
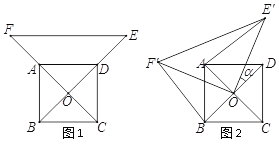
【題目】如圖1,已知![]() 為正方形
為正方形![]() 的中心,分別延長
的中心,分別延長![]() 到點
到點![]() ,
, ![]() 到點
到點![]() ,使
,使![]() ,
, ![]() ,連結
,連結![]() ,將△
,將△![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 角得到△
角得到△![]() (如圖2).連結
(如圖2).連結![]() 、
、![]() .
.
(Ⅰ)探究![]() 與
與![]() 的數量關系,并給予證明;
的數量關系,并給予證明;
(Ⅱ)當![]() ,
, ![]() 時,求:
時,求:
①![]() 的度數;
的度數;
②![]() 的長度.
的長度.
【答案】(1)證明見解析(2)①30°②![]()
【解析】(1)首先證明△AOE′≌△BOF′,根據全等三角形的對應邊相等,即可證得;
(2)①延長OA到M,使AM=OA,則OM=OE′.易證△OME′是等邊三角形,據此∠AE′O的度數即可求得;②在直角△AOB中,利用三角函數即可求得OB的長,然后在直角△OBF′中利用三角函數求得BF′的長.
本題解析:如圖:
(1)∵正方形ABCD中,OA=OD=OB,
又∵OF=2OA,OE=2OD,
∴OE=OF,則OE′=OF′,
在△AOE′和△BOF′中,
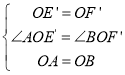
∴△AOE′≌△BOF′
∴AE′=BF′;
(2)①延長OA到M,使AM=OA,則OM=OE′.
∵正方形ABCD中,∠AOD=90°,
∴∠AOE′=90°﹣30°=60°,
∴△OME′是等邊三角形,
又∵AM=OA,
∴AE′⊥OM,
則∠E′AO=90°,
∴∠AOE′=90°﹣α=60°,
∴在直角△AOE′中,∠AE′O=90°﹣∠AOE′=30°;
②∵∠AOE′=90°﹣α=60°,∠E′OF′=90°,
∴∠AOF′=30°,
又∵∠AOB=90°,
∴∠BOF′=60°,
又∵等腰直角△AOB中,OB=![]() AB=
AB=![]() ,
,
∴在Rt△ABE'中得到AE'=![]() OA=
OA=![]() ,
,
又BF'=AE'
∴BF′=![]() .
.


科目:初中數學 來源: 題型:
【題目】數學課上,李老師出示了如下的題目:
“在等邊三角形ABC中,點E在AB上,點D在CB的延長線上,且ED=EC,如圖,試確定線段AE與DB的大小關系,并說明理由”.
小敏與同桌小聰討論后,進行了如下解答:
(1)特殊情況,探索結論
當點E為AB的中點時,如圖1,確定線段AE與DB的大小關系,請你直接寫出結論:AEDB(填“>”,“<”或“=”).
(2)特例啟發,解答題目
解:題目中,AE與DB的大小關系是:AE DB(填“>”,“<”或“=”).理由如下:如圖2,過點E作EF∥BC,交AC于點F.(請你完成以下解答過程)
(3)拓展結論,設計新題
在等邊三角形ABC中,點E在直線AB上,點D在直線BC上,且ED=EC.若△ABC的邊長為1,AE=2,CD= (請你直接寫出結果).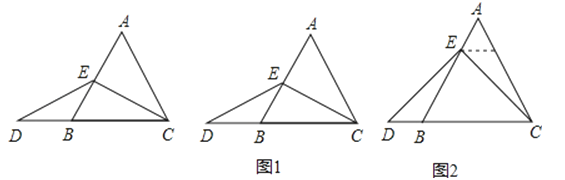
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com