
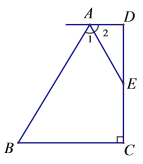
【題目】如圖,已知AD∥BC,DC⊥BC, AE平分∠BAD, E為CD中點,試探索AD、BC和AB之間有何關系?并說明理由.
【答案】AD+BC=AB見解析;
【解析】
利用“AAS”可證明Rt△ADE≌Rt△AFE得到AD=AF,利用“HL”可證明Rt△BCE≌Rt△BFE得到BC=BF,于是有AD+BC=AF+BF=AB.
證明:過點E作EF⊥AB,連接BE
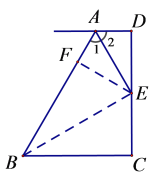
∵AD∥BC,DC⊥BC, EF⊥AB
∴∠D+∠C=180°,∠C=∠AFE=∠BFE=90°
∴∠D=∠AFE =90°.
∵AE平分∠BAD,
∴∠1=∠2
在△ADE和△AFE中
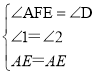
∴△ADE≌△AFE(AAS),
∴FE=DE,AD=AF
又∵E為CD中點
∴DE=CE,
∴FE =CE,
在Rt△BEF和Rt△BEC中,![]()
![]()
∴Rt△ BEF≌Rt△ BEC(HL),
∴BF= BC
∴AD+BC=AF+BF=AB.


 名校通行證有效作業(yè)系列答案
名校通行證有效作業(yè)系列答案科目:初中數(shù)學 來源: 題型:
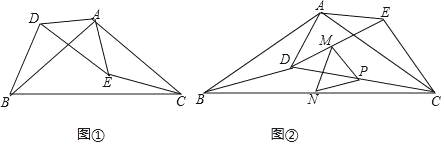
【題目】如圖①,在等腰△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE=120°.
(1)求證:△ABD≌△ACE;
(2)把△ADE繞點A逆時針方向旋轉到圖②的位置,連接CD,點M、P、N分別為DE、DC、BC的中點,連接MN、PN、PM,判斷△PMN的形狀,并說明理由;
(3)在(2)中,把△ADE繞點A在平面內自由旋轉,若AD=4,AB=6,請分別求出△PMN周長的最小值與最大值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在每個小正方形的邊長為1的網(wǎng)格中,點A、B、C均在格點上,在△ABC的內部有一點P,滿足S△PAB:S△PBC:S△PCA=1:2:3,請在如圖所示的網(wǎng)格中,用無刻度直尺畫出點P(保留畫圖痕跡)
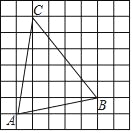
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】把下列各數(shù)﹣5,|﹣1.5|,﹣![]() ,0,3
,0,3![]() ,﹣(﹣1)表示的點.
,﹣(﹣1)表示的點.
(1)畫在數(shù)軸上;
(2)用“<”把這些數(shù)連接起來;
(3)指出:負數(shù)是 ;分數(shù)是 ;非負整數(shù)是 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】公元3世紀,古希臘數(shù)學家丟番圖(Diophantus)在其《算術》一書中設置了以下問題:已知兩正整數(shù)之和為20,乘積為96,求這兩個數(shù).因為兩數(shù)之和為20,所以這兩個數(shù)不可能同時大于10,也不可能同時小于10,必定是一個大于10,一個小于10.根據(jù)如圖所示的設法,可設一個數(shù)為![]() ,則另一個數(shù)為
,則另一個數(shù)為![]() ,根據(jù)兩數(shù)之積為96,可得
,根據(jù)兩數(shù)之積為96,可得![]() .請根據(jù)以上思路解決下列問題:
.請根據(jù)以上思路解決下列問題:
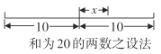
(1)若兩個正整數(shù)之和為100,大數(shù)比小數(shù)大![]() ,根據(jù)丟番圖的設法,這兩個正整數(shù)可表示為____和___;
,根據(jù)丟番圖的設法,這兩個正整數(shù)可表示為____和___;
(2)請你根據(jù)丟番圖的運算方法,計算![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
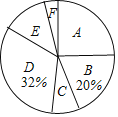
【題目】某校為了解學生最喜歡的球類運動情況,隨機選取該校部分學生進行調查,要求每名學生只寫一類最喜歡的球類運動.以下是根據(jù)調查結果繪制的統(tǒng)計圖表的一部分.
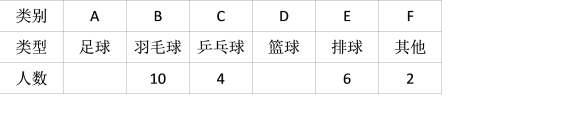
根據(jù)以上信息,解答下列問題:
(1)被調查的學生中,最喜歡乒乓球的有 人,最喜歡籃球的學生數(shù)占被調查總人數(shù)的百分比為 %;
(2)被調查學生的總數(shù)為 人,其中,最喜歡籃球的有 人,最喜歡足球的學生數(shù)占被調查總人數(shù)的百分比為 %;
(3)該校共有450名學生,根據(jù)調查結果,估計該校最喜歡排球的學生數(shù).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
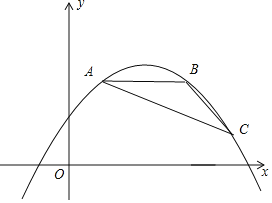
【題目】如圖,點A,B,C都在拋物線y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x軸,∠ABC=135°,且AB=4.
<a<0)上,AB∥x軸,∠ABC=135°,且AB=4.
(1)填空:拋物線的頂點坐標為 (用含m的代數(shù)式表示);
(2)求△ABC的面積(用含a的代數(shù)式表示);
(3)若△ABC的面積為2,當2m﹣5≤x≤2m﹣2時,y的最大值為2,求m的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,數(shù)軸上![]() 兩點對應的數(shù)分別為
兩點對應的數(shù)分別為![]() 、16,點
、16,點![]() 為數(shù)軸上一動點,點
為數(shù)軸上一動點,點![]() 對應的數(shù)為
對應的數(shù)為![]() .
.
(1)填空:若![]() 時,點
時,點![]() 到點
到點![]() 、點
、點![]() 的距離之和為_____________.
的距離之和為_____________.
(2)填空:若點![]() 到點
到點![]() 、點
、點![]() 的距離相等,則
的距離相等,則![]() _______.
_______.
(3)填空:若![]() ,則
,則![]() _______.
_______.
(4)若動點![]() 以每秒2個單位長度的速度從點
以每秒2個單位長度的速度從點![]() 向點
向點![]() 運動,動點
運動,動點![]() 以每秒3個單位長度的速度從點
以每秒3個單位長度的速度從點![]() 向點
向點![]() 運動兩動點同時運動且一動點到達終點時另一動點也停止運動,經(jīng)過
運動兩動點同時運動且一動點到達終點時另一動點也停止運動,經(jīng)過![]() 秒
秒![]() ,求
,求![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】下列語句:①-1是1的平方根。②帶根號的數(shù)都是無理數(shù)。③-1的立方根是-1。④![]() 的立方根是2。⑤(-2)2的算術平方根是2。⑥-125的立方根是±5。⑦有理數(shù)和數(shù)軸上的點一一對應。其中正確的有( )
的立方根是2。⑤(-2)2的算術平方根是2。⑥-125的立方根是±5。⑦有理數(shù)和數(shù)軸上的點一一對應。其中正確的有( )
A. 2個B. 3個C. 4個D. 5個
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com