
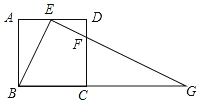
【題目】如圖,在正方形ABCD中,E、F分別是邊AD、CD上的點,AE=ED,DC=4DF,連接EF并延長交BC的延長線于點G.
(1)求證:△ABE∽△DEF;
(2)若正方形的邊長為16,求BG的長.
 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,王老師將某班近三個月跳躍類項目的訓練情況做了統計,并繪制了折線統計圖,則根據圖中信息以下判斷錯誤的是( )
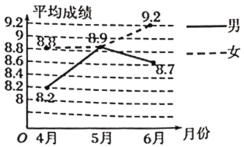
A.男女生5月份的平均成績一樣
B.4月到6月,女生平均成績一直在進步
C.4月到5月,女生平均成績的增長率約為![]()
D.5月到6月女生平均成績比4月到5月的平均成績增長快
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了發展鄉村旅游,建設美麗鄉村,某中學七年級(1)班同學都積極參加了植樹活動,將今年三月份該班同學的植樹情況繪制成如圖所示的不完整的統計圖.已知植樹量為2株的人數占總人數的32%.
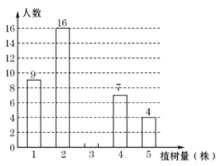
(1)該班的總人數為____________,植樹株數的眾數是____________,植樹株數的中位數是____________;
(2)請將條形統計圖補充完整;
(3)若將該班同學的植樹情況繪制成扇形統計圖,求“植樹量為3株”所對應的扇形的園心角度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
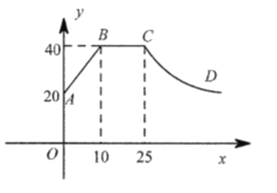
【題目】一般情況下,學生注意力上課后逐漸增強,中間有段時間處于較理想的穩定狀態,隨后開始分散.實驗結果表明,學生注意力指數y隨時間x(min)的變化規律如圖所示(其中![]() 分別為線段,
分別為線段,![]() 為雙曲線的一部分):
為雙曲線的一部分):
(1)上課后第![]() 與第
與第![]() 相比較,何時學生注意力更集中?
相比較,何時學生注意力更集中?
(2)某道難題需連續講![]() ,為保證效果,學生注意力指數不宜低于
,為保證效果,學生注意力指數不宜低于![]() ,老師能否在所需要求下講完這道題?
,老師能否在所需要求下講完這道題?
查看答案和解析>>
科目:初中數學 來源: 題型:
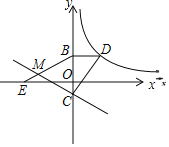
【題目】如圖,已知點D在反比例函數![]() 的圖象上,過點D作x軸的平行線交y軸于點B(0,2),過點A(
的圖象上,過點D作x軸的平行線交y軸于點B(0,2),過點A(![]() ,0)的直線y=kx+b與y軸于點C,且BD=2OC,tan∠OAC=
,0)的直線y=kx+b與y軸于點C,且BD=2OC,tan∠OAC=![]() .
.
(1)求反比例函數![]() 的解析式;
的解析式;
(2)連接CD,試判斷線段AC與線段CD的關系,并說明理由;
(3)點E為x軸上點A左側的一點,且AE=BD,連接BE交直線CA于點M,求tan∠BMC的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),已知點G在正方形ABCD的對角線AC上,GE⊥BC,垂足為點E,GF⊥CD,垂足為點F.
(1)證明與推斷:
①求證:四邊形CEGF是正方形;
②推斷:![]() 的值為 :
的值為 :
(2)探究與證明:
將正方形CEGF繞點C順時針方向旋轉α角(0°<α<45°),如圖(2)所示,試探究線段AG與BE之間的數量關系,并說明理由:
(3)拓展與運用:
正方形CEGF在旋轉過程中,當B,E,F三點在一條直線上時,如圖(3)所示,延長CG交AD于點H.若AG=6,GH=2![]() ,則BC= .
,則BC= .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:對于任意正實數a、b,∵![]() ≥0, ∴
≥0, ∴![]() ≥0,
≥0,
∴![]() ≥
≥![]() ,只有當a=b時,等號成立.
,只有當a=b時,等號成立.
結論:在![]() ≥
≥![]() (a、b均為正實數)中,若ab為定值p,則a+b≥
(a、b均為正實數)中,若ab為定值p,則a+b≥![]() ,只有當a=b時,a+b有最小值
,只有當a=b時,a+b有最小值![]() .
.
根據上述內容,回答下列問題:
若m>0,只有當m= 時,![]() 有最小值 .
有最小值 .
思考驗證:如圖1,AB為半圓O的直徑,C為半圓上任意一點(與點A、B不重合),過點C作CD⊥AB,垂足為D,AD=a,DB=b.
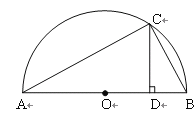
試根據圖形驗證![]() ≥
≥![]() ,并指出等號成立時的條件.
,并指出等號成立時的條件.
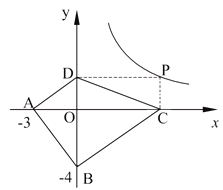
探索應用:如圖2,已知A(-3,0),B(0,-4),P為雙曲線![]() (x>0)上的任意一點,過點P作PC⊥x軸于點C,PD⊥y軸于點D.求四邊形ABCD面積的最小值,并說明此時四邊形ABCD的形狀.
(x>0)上的任意一點,過點P作PC⊥x軸于點C,PD⊥y軸于點D.求四邊形ABCD面積的最小值,并說明此時四邊形ABCD的形狀.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,點
,點![]() 、
、![]() 同時從點
同時從點![]() 出發,以
出發,以![]() 的速度分別沿
的速度分別沿![]() 、
、![]() 勻速運動,當點
勻速運動,當點![]() 到達點
到達點![]() 時,兩點同時停止運動,設運動時間為
時,兩點同時停止運動,設運動時間為![]() .過點
.過點![]() 作
作![]() 的垂線
的垂線![]() 交
交![]() 于點
于點![]() ,點
,點![]() 與點
與點![]() 關于直線
關于直線![]() 對稱.
對稱.
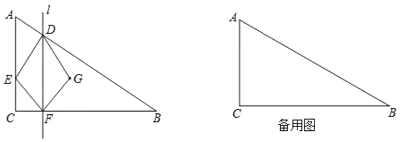
(1)當![]() _____
_____![]() 時,點
時,點![]() 在
在![]() 的平分線上;
的平分線上;
(2)當![]() _____
_____![]() 時,點
時,點![]() 在
在![]() 邊上;
邊上;
(3)設![]() 與
與![]() 重合部分的面積為
重合部分的面積為![]() ,求
,求![]() 與
與![]() 之間的函數關系式,并寫
之間的函數關系式,并寫![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com