
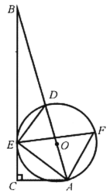
【題目】如圖,在矩形ABCD中,AB=6,BC=![]() ,E為CD邊上一點(diǎn),將△BCE沿BE折疊,點(diǎn)C的對(duì)應(yīng)點(diǎn)為點(diǎn)F,連接AF,若
,E為CD邊上一點(diǎn),將△BCE沿BE折疊,點(diǎn)C的對(duì)應(yīng)點(diǎn)為點(diǎn)F,連接AF,若![]() ,則CE=__________.
,則CE=__________.

【答案】![]()
【解析】
已知![]() ,可作輔助線構(gòu)造直角三角形,設(shè)未知數(shù),利用勾股定理可求出FM、BM,進(jìn)而求出FN,再利用三角形相似和折疊的性質(zhì)求出EC.
,可作輔助線構(gòu)造直角三角形,設(shè)未知數(shù),利用勾股定理可求出FM、BM,進(jìn)而求出FN,再利用三角形相似和折疊的性質(zhì)求出EC.
解:過點(diǎn)F作MN∥AD,交AB、CD分別于點(diǎn)M、N,則MN⊥AB,MN⊥CD,
∴∠FNE=∠BMF=90°
∴∠NFE+∠NEF=90°
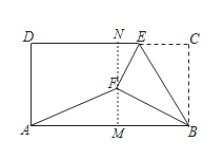
由折疊得:EC=EF,BC=BF=![]() ,∠C=∠BFE=90°,
,∠C=∠BFE=90°,
∴∠NFE+∠BFM=90°
∴∠MFB=∠NEF
∵![]()
∴設(shè)FM=x,則AM=3x,![]() ,
,
∴![]()
在Rt△BFM中,由勾股定理得:![]()
解得:![]()
∵![]()
∴x=1
∴FM=1,AM=BM=3,
∵∠FNE=∠BMF=90°, ∠MFB=∠NEF
∴△BMF∽△FNE,
∴![]()
∴![]()
∴EF=![]()
故答案為: ![]()


 全能練考卷系列答案
全能練考卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某公司推出一款產(chǎn)品,經(jīng)市場(chǎng)調(diào)查發(fā)現(xiàn),該產(chǎn)品的日銷售量y(個(gè))與銷售單價(jià)x(元)之間滿足一次函數(shù)關(guān)系.關(guān)于銷售單價(jià),日銷售量,日銷售利潤(rùn)的幾組對(duì)應(yīng)值如下表:
銷售單價(jià)x(元) | 85 | 95 | 105 | 115 |
日銷售量y(個(gè)) | 175 | 125 | 75 | m |
日銷售利潤(rùn)w(元) | 875 | 1875 | 1875 | 875 |
(注:日銷售利潤(rùn)=日銷售量×(銷售單價(jià)﹣成本單價(jià)))
(1)求y關(guān)于x的函數(shù)解析式(不要求寫出x的取值范圍)及m的值;
(2)根據(jù)以上信息,填空:
該產(chǎn)品的成本單價(jià)是 元,當(dāng)銷售單價(jià)x= 元時(shí),日銷售利潤(rùn)w最大,最大值是 元;
(3)公司計(jì)劃開展科技創(chuàng)新,以降低該產(chǎn)品的成本,預(yù)計(jì)在今后的銷售中,日銷售量與銷售單價(jià)仍存在(1)中的關(guān)系.若想實(shí)現(xiàn)銷售單價(jià)為90元時(shí),日銷售利潤(rùn)不低于3750元的銷售目標(biāo),該產(chǎn)品的成本單價(jià)應(yīng)不超過多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了解市民“獲取新聞的最主要途徑”,某市記者開展了一次抽樣調(diào)查,要求被調(diào)查的市民必選且只能選一項(xiàng).根據(jù)調(diào)查結(jié)果繪制了如圖尚不完整的扇形統(tǒng)計(jì)圖,其中將“手機(jī)上網(wǎng)”和“電腦上網(wǎng)”作為“獲取新聞的最主要途徑”的市民分別有600人和510人,并且扇形統(tǒng)計(jì)圖中![]() ,
,![]() 滿足
滿足![]() .請(qǐng)根據(jù)所給信息,解答下列問題:
.請(qǐng)根據(jù)所給信息,解答下列問題:

(1)請(qǐng)計(jì)算扇形統(tǒng)計(jì)圖中“電腦上網(wǎng)”所在扇形的圓心角的度數(shù);
(2)求扇形統(tǒng)計(jì)圖中![]() ,
,![]() 的值;
的值;
(3)若該市約有200萬人,請(qǐng)你估計(jì)其中將“手機(jī)上網(wǎng)”和“報(bào)紙”作為“獲取新聞的最主要途徑”的總?cè)藬?shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知拋物線![]() 過點(diǎn)A(﹣3,0),B(﹣2,3),C(0,3),其頂點(diǎn)為D.
過點(diǎn)A(﹣3,0),B(﹣2,3),C(0,3),其頂點(diǎn)為D.
(1)求拋物線的解析式;
(2)設(shè)點(diǎn)M(1,m),當(dāng)MB+MD的值最小時(shí),求m的值;
(3)若P是拋物線上位于直線AC上方的一個(gè)動(dòng)點(diǎn),求△APC的面積的最大值;
(4)若拋物線的對(duì)稱軸與直線AC相交于點(diǎn)N,E為直線AC上任意一點(diǎn),過點(diǎn)E作EF∥ND交拋物線于點(diǎn)F,以N,D,E,F為頂點(diǎn)的四邊形能否為平行四邊形?若能,求點(diǎn)E的坐標(biāo);若不能,請(qǐng)說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,等邊三角形![]() 中,D是
中,D是![]() 上一點(diǎn),連接
上一點(diǎn),連接![]() 并將
并將![]() 繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)120°得到線段
繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)120°得到線段![]() ,連接
,連接![]() 交
交![]() 于點(diǎn)F.
于點(diǎn)F.
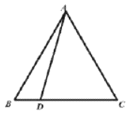
(1)當(dāng)點(diǎn)D為![]() 中點(diǎn),且
中點(diǎn),且![]() 時(shí),
時(shí),![]() ___________;
___________;
(2)補(bǔ)全圖形,探究線段![]() 與
與![]() 之間的數(shù)量關(guān)系,并證明你的結(jié)論.
之間的數(shù)量關(guān)系,并證明你的結(jié)論.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一次函數(shù)![]() 的圖象分別交x軸、y軸于C,D兩點(diǎn),交反比例函數(shù)
的圖象分別交x軸、y軸于C,D兩點(diǎn),交反比例函數(shù)![]() 圖象于A(
圖象于A(![]() ,4),B(3,m)兩點(diǎn).
,4),B(3,m)兩點(diǎn).
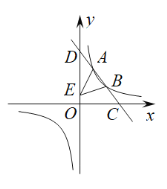
(1)求直線CD的表達(dá)式;
(2)點(diǎn)E是線段OD上一點(diǎn),若![]() ,求E點(diǎn)的坐標(biāo);
,求E點(diǎn)的坐標(biāo);
(3)請(qǐng)你根據(jù)圖象直接寫出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在方格紙中(小正方形的邊長(zhǎng)為1個(gè)單位長(zhǎng)度),點(diǎn)![]() ,
,![]() ,
,![]() 都在格點(diǎn)上,以
都在格點(diǎn)上,以![]() 為坐標(biāo)原點(diǎn)建立平面直角坐標(biāo)系.
為坐標(biāo)原點(diǎn)建立平面直角坐標(biāo)系.
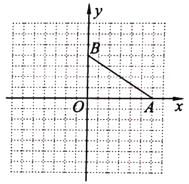
(1)分別寫出點(diǎn)![]() ,
,![]() 的坐標(biāo):________,畫出線段
的坐標(biāo):________,畫出線段![]() 繞著點(diǎn)
繞著點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)
逆時(shí)針旋轉(zhuǎn)![]() 的線段
的線段![]() ;
;
(2)若線段![]() 的中點(diǎn)
的中點(diǎn)![]() 在反比例函數(shù)
在反比例函數(shù)![]()
![]() 的圖象上,則
的圖象上,則![]() 的值為________.(直接寫出答案)
的值為________.(直接寫出答案)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 是
是![]() 上一點(diǎn),經(jīng)過
上一點(diǎn),經(jīng)過![]() ,
,![]() 兩點(diǎn)的
兩點(diǎn)的![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() ,作
,作![]() 的平分線
的平分線![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() .
.
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)若![]() ,
,![]() ,求線段
,求線段![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,A1(1,![]() ),A2(
),A2(![]() ,
,![]() ),A3(2,
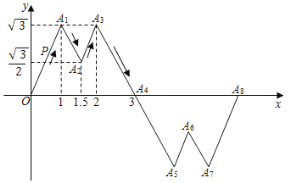
),A3(2,![]() ),A4(3,0).作折線A1A2A3A4關(guān)于點(diǎn)A4的中心對(duì)稱圖形,再做出新的折線關(guān)于與x軸的下一個(gè)交點(diǎn)的中心對(duì)稱圖形……以此類推,得到一個(gè)大的折線.現(xiàn)有一動(dòng)點(diǎn)P從原點(diǎn)O出發(fā),沿著折線一每秒1個(gè)單位的速度移動(dòng),設(shè)運(yùn)動(dòng)時(shí)間為t.當(dāng)t=2020時(shí),點(diǎn)P的坐標(biāo)為( )
),A4(3,0).作折線A1A2A3A4關(guān)于點(diǎn)A4的中心對(duì)稱圖形,再做出新的折線關(guān)于與x軸的下一個(gè)交點(diǎn)的中心對(duì)稱圖形……以此類推,得到一個(gè)大的折線.現(xiàn)有一動(dòng)點(diǎn)P從原點(diǎn)O出發(fā),沿著折線一每秒1個(gè)單位的速度移動(dòng),設(shè)運(yùn)動(dòng)時(shí)間為t.當(dāng)t=2020時(shí),點(diǎn)P的坐標(biāo)為( )
A.(1010,![]() )B.(2020,
)B.(2020,![]() )C.(2016,0)D.(1010,
)C.(2016,0)D.(1010,![]() )
)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com