
【題目】已知如圖1,在以O為原點的平面直角坐標系中,拋物線y= ![]() x2+bx+c與x軸交于A、B兩點,與y軸交于點C(0,﹣1),連接AC,AO=2CO,直線l過點G(0,t)且平行于x軸,t<﹣1,
x2+bx+c與x軸交于A、B兩點,與y軸交于點C(0,﹣1),連接AC,AO=2CO,直線l過點G(0,t)且平行于x軸,t<﹣1,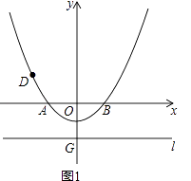
(1)求拋物線對應的二次函數的解析式;
(2)若D為拋物線y= ![]() x2+bx+c上一動點,是否存在直線l使得點D到直線l的距離與OD的長恒相等?若存在,求出此時t的值;
x2+bx+c上一動點,是否存在直線l使得點D到直線l的距離與OD的長恒相等?若存在,求出此時t的值;
(3)如圖2,若E、F為上述拋物線上的兩個動點,且EF=8,線段EF的中點為M,求點M縱坐標的最小值.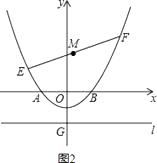
【答案】
(1)
解:∵c(0,﹣1),
∴y= ![]() x2+bx﹣1,
x2+bx﹣1,
又∵AO=2OC,
∴點A坐標為(﹣2,0),
代入得:1﹣2b﹣1=0,
解得:b=0,
∴解析式為:y= ![]() x2﹣1
x2﹣1
(2)
解:假設存在直線l使得點D到直線l的距離與OD的長恒相等,
設D(a, ![]() a2﹣1),
a2﹣1),
則OD= ![]() =
= ![]() =
= ![]() a2+1,
a2+1,
點D到直線l的距離: ![]() a2﹣1+|t|,
a2﹣1+|t|,
∴ ![]() a2﹣1+|t|=
a2﹣1+|t|= ![]() a2+1,
a2+1,
解得:|t|=2,
∵t<﹣1,
∴t=﹣2,
故當t=﹣2時,直線l使得點D到直線l的距離與OD的長恒相等
(3)
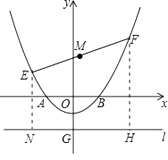
解:作EN⊥直線l于點N,FH⊥直線l于點H,
設E(x1,y1),F(x2,y2),
則EN=y1+2,FH=y2+2,
∵M為EF中點,
∴M縱坐標為: ![]() =
= ![]() =
= ![]() ﹣2,
﹣2,
由(2)得:EN=OE,FH=OF,
∴ ![]() =
= ![]() ﹣2=
﹣2= ![]() ﹣2,
﹣2,
要使M縱坐標最小,即 ![]() ﹣2最小,
﹣2最小,
當EF過點O時,OE+OF最小,最小值為8,
∴M縱坐標最小值為 ![]() ﹣2=
﹣2= ![]() ﹣2=2.
﹣2=2.
【解析】(1)根據點C坐標,可得c=﹣1,然后根據AO=2CO,可得出點A坐標,將點A坐標代入求出b值,即可得出函數解析式;(2)假設存在直線l使得點D到直線l的距離與OD的長恒相等,設出點D坐標,分別求出OD和點D到直線l的距離,然后列出等式求出t的值;(3)作EN⊥直線l于點G,FH⊥直線l于點H,設出點E、F坐標,表示出點M的縱坐標,根據(2)中得出的結果,代入結果求出M縱坐標的最小值.
【考點精析】解答此題的關鍵在于理解二次函數的圖象的相關知識,掌握二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點,以及對二次函數的性質的理解,了解增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,△ABC的三個頂點坐標分別為A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)①畫出△ABC關于y軸對稱的△A1B1C1;
②畫出△ABC關于原點O成中心對稱的△A2B2C2;
(2)求△A2B2C2的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 是等邊
是等邊![]() 內一點,
內一點, ![]() .將
.將![]() 繞點
繞點![]() 按順時針方向旋轉
按順時針方向旋轉![]() 得
得![]() ,連接
,連接![]() .
.

(1)求證: ![]() 是等邊三角形;
是等邊三角形;
(2)當![]() 時,試判斷
時,試判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
(3)探究:當![]() 為多少度時,
為多少度時, ![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為鼓勵居民節約用電,我市自2012年以來對家庭用電收費實行階梯電價,即每月對每戶居民的用電量分為三個檔級收費,第一檔為用電量在180千瓦時(含180千瓦時)以內的部分,執行基本價格;第二檔為用電量在180千瓦時到450千瓦時(含450千瓦時)的部分,實行提高電價;第三檔為用電量超出450千瓦時的部分,執行市場調節價格. 我市一位同學家今年2月份用電330千瓦時,電費為213元,3月份用電240千瓦時,電費為150元.已知我市的一位居民今年4、5月份的家庭用電量分別為160和 410千瓦時,請你依據該同學家的繳費情況,計算這位居民4、5月份的電費分別為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠B=60°,對角線AC平分角∠BAD,點P是△ABC內一點,連接PA、PB、PC,若PA=6,PB=8,PC=10,則菱形ABCD的面積等于_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
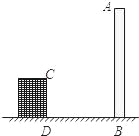
【題目】我市在城市建設中,要折除舊煙囪AB(如圖所示),在煙囪正西方向的樓CD的頂端C,測得煙囪的頂端A的仰角為45°,底端B的俯角為30°,已量得DB=21m.
(1)在原圖上畫出點C望點A的仰角和點C望點B的俯角,并分別標出仰角和俯角的大小;
(2)拆除時若讓煙囪向正東倒下,試問:距離煙囪正東35m遠的一棵大樹是否被歪倒的煙囪砸著?請說明理由.(![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】當三角形中一個內角是另一個內角的3倍時,我們稱此三角形為“夢想三角形”.如果一個“夢想三角形”有一個角為108°,那么這個“夢想三角形”的最小內角的度數為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程2x2﹣(4k+2)x+2k2+1=0.
(1)當k取何值時,方程有兩個不相等的實數根?
(2)當k取何值時,方程有兩個相等的實數根?
(3)當k取何值時,方程沒有實數根?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com