
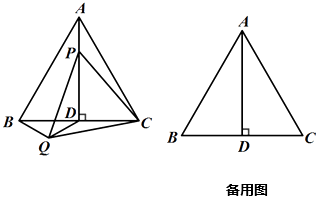
【題目】如圖,正△ABC 中,高線 ![]() ,點
,點 ![]() 從點
從點 ![]() 出發,沿著
出發,沿著 ![]() 運動到點
運動到點 ![]() 停止,以
停止,以 ![]() 為邊向左下方作正
為邊向左下方作正 ![]() ,連接
,連接 ![]() ,
, ![]() .
.
(1)求證: ![]() ≌
≌ ![]() ;
;
(2)在點P的運動過程中,當 ![]() 是等腰三角形時,求
是等腰三角形時,求 ![]() 的度數;
的度數;
(3)直接寫出在點 P的運動過程中, ![]() 的最小值.
的最小值.
【答案】
(1)
證明:∵![]() ABC和
ABC和![]() PQC是正三角形,∴AC=BC,PC=QC,
PQC是正三角形,∴AC=BC,PC=QC,![]() ACB=
ACB=![]() PCQ=60
PCQ=60![]() ,
,
又∵![]() ACP=60
ACP=60![]() -
-![]() BCP,
BCP,![]() BCP=60
BCP=60![]() -
-![]() BCP,∴
BCP,∴![]() ACP=
ACP=![]() BCP.
BCP.
在![]() ACP和
ACP和![]() BCQ中,
BCQ中,
∵ ,
,
∴![]() ACP
ACP![]()
![]() BCQ(SAS).
BCQ(SAS).
(2)
解:由(1)知,![]() ACP
ACP![]()
![]() BCQ,∴
BCQ,∴![]() QBD=
QBD=![]() PAC=30
PAC=30![]() ,
,
當ΔBDQ 是等腰三角形時,
①若BQ=QD,,如圖1,則![]() BDQ=30
BDQ=30![]() ;
;

圖1
②若BQ=BD,如圖2,則![]() BDQ=75
BDQ=75![]() ;
;
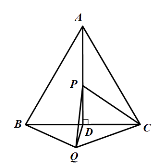
圖2
③若BD=DQ,如圖3,則![]() BDQ=120
BDQ=120![]() .
.

圖3
答:![]() BDQ的度數為30
BDQ的度數為30![]() 或75
或75![]() 或120
或120![]() .
.
(3)![]()
【解析】(3)解:如圖4,過點P作PM![]() AB于點M,
AB于點M,
圖4
∵![]() BAD=30
BAD=30![]() ,PM=
,PM=![]() AP,即:AP=2PM,
AP,即:AP=2PM,
∴AP+2PC=2PM+2PC=2(PM+PC),
∴當AP+2PC最小時,即2PM+2PC最小,即PM+PC最小. ∴當點P運動到P、C、M在同一直線上時,PM+PC最小.
過點C作CN![]() AB于點N,
AB于點N,
當點P運動到CN與AD的交點處時,PM+PC最小,最小值為等邊三角形ABC的高CN=6,
∴AP+2PC的最小值=2![]() 6=12.
6=12.
【考點精析】利用等腰三角形的性質和軸對稱-最短路線問題對題目進行判斷即可得到答案,需要熟知等腰三角形的兩個底角相等(簡稱:等邊對等角);已知起點結點,求最短路徑;與確定起點相反,已知終點結點,求最短路徑;已知起點和終點,求兩結點之間的最短路徑;求圖中所有最短路徑.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】在銳角△ABC中,AB=AC,AD為BC邊上的高,E為AC中點.
(1)如圖1,過點C作CF⊥AB于F點,連接EF.若∠BAD=20°,求∠AFE的度數;
(2)若M為線段BD上的動點(點M與點D不重合),過點C作CN⊥AM于N點,射線EN,AB交于P點.
①依題意將圖2補全;
②小宇通過觀察、實驗,提出猜想:在點M運動的過程中,始終有∠APE=2∠MAD.
小宇把這個猜想與同學們進行討論,形成了證明該猜想的幾種想法:
想法1:連接DE,要證∠APE=2∠MAD,只需證∠PED=2∠MAD.
想法2:設∠MAD=α,∠DAC=β,只需用α,β表示出∠PEC,通過角度計算得∠APE=2α.
想法3:在NE上取點Q,使∠NAQ=2∠MAD,要證∠APE=2∠MAD,只需證△NAQ∽△APQ.……
請你參考上面的想法,幫助小宇證明∠APE =2∠MAD.(一種方法即可)
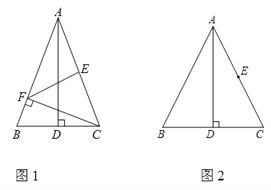
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某餐廳中,一張桌子可坐6人,有以下兩種擺放方式:
(1)有4張桌子,用第一種擺設方式,可以坐 人;用第二種擺設方式,可以坐 人;
(2)有n張桌子,用第一種擺設方式可以坐 人;用第二種擺設方式,可以坐 人(用含有n的代數式表示);
(3)一天中午,餐廳要接待120位顧客共同就餐,但餐廳中只有30張這樣的長方形桌子可用,且每6張拼成一張大桌子,若你是這家餐廳的經理,你打算選擇哪種方式來擺放餐桌,為什么?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中, ![]() ,點P在邊
,點P在邊 ![]() 上,且滿足
上,且滿足 ![]() .
.

(1)畫出點P的位置(尺規作圖,保留痕跡);
(2)①若 ![]() ,
, ![]() ,則
,則 ![]() 的周長為;
的周長為;
②若 ![]() ,則
,則 ![]() °.
°.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=![]() x2+bx﹣2與x軸交于A、B兩點,與y軸交于C點,且A(﹣1,0).
x2+bx﹣2與x軸交于A、B兩點,與y軸交于C點,且A(﹣1,0).
(1)求拋物線的解析式及頂點D的坐標;
(2)判斷△ABC的形狀,證明你的結論;
(3)點M是x軸上的一個動點,當△DCM的周長最小時,求點M的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:已知點A、B是反比例函數y=﹣![]() 上在第二象限內的分支上的兩個點,點C(0,3),且△ABC滿足AC=BC,∠ACB=90°,則線段AB的長為__.
上在第二象限內的分支上的兩個點,點C(0,3),且△ABC滿足AC=BC,∠ACB=90°,則線段AB的長為__.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一種拉桿式旅行箱的示意圖如圖所示,箱體長AB=50cm,拉桿最大伸長距離BC=35cm,(點A、B、C在同一條直線上),在箱體的底端裝有一圓形滾輪⊙A,⊙A與水平地面切于點D,AE∥DN,某一時刻,點B距離水平面38cm,點C距離水平面59cm.
(1)求圓形滾輪的半徑AD的長;
(2)當人的手自然下垂拉旅行箱時,人感覺較為舒服,已知某人的手自然下垂在點C處且拉桿達到最大延伸距離時,點C距離水平地面73.5cm,求此時拉桿箱與水平面AE所成角∠CAE的大小(精確到1°,參考數據:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
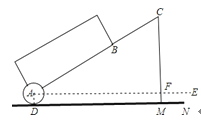
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】規定※是一種新的運算符號,且a※b=ab+a+b,例如:2※3=2×3+2+3=11,那么(3※4)※1=( )
A.19
B.29
C.39
D.49
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com