
【題目】列分式方程解應(yīng)用題:
“5G改變世界,5G創(chuàng)造未來”.2019年9月,全球首個(gè)5G上海虹橋火車站,完成了5G網(wǎng)絡(luò)深度覆蓋,旅客可享受到高速便捷的5G網(wǎng)絡(luò)服務(wù).虹橋火車站中5G網(wǎng)絡(luò)峰值速率為4G網(wǎng)絡(luò)峰值速率的10倍.在峰值速率下傳輸7千兆數(shù)據(jù),5G網(wǎng)絡(luò)比4G網(wǎng)絡(luò)快630秒,求5G網(wǎng)絡(luò)的峰值速率.
【答案】5G網(wǎng)絡(luò)的峰值速率為每秒傳輸0.1千兆數(shù)據(jù).
【解析】
設(shè)4G網(wǎng)絡(luò)的峰值速率為每秒傳輸x千兆,則5G網(wǎng)絡(luò)的峰值速率為每秒傳輸10x千兆,根據(jù)在峰值速率下傳輸7千兆數(shù)據(jù),5G網(wǎng)絡(luò)快630秒列出方程即可.
解:設(shè)4G網(wǎng)絡(luò)的峰值速率為每秒傳輸![]() 千兆數(shù)據(jù),則5G網(wǎng)絡(luò)的峰值速率為每秒傳輸10x千兆.
千兆數(shù)據(jù),則5G網(wǎng)絡(luò)的峰值速率為每秒傳輸10x千兆.
依題意,得![]()
解得 ![]() .
.
經(jīng)檢驗(yàn):![]() 是原方程的解,且滿足實(shí)際意義.
是原方程的解,且滿足實(shí)際意義.
![]()
答:5G網(wǎng)絡(luò)的峰值速率為每秒傳輸![]() 千兆數(shù)據(jù).
千兆數(shù)據(jù).


 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點(diǎn)A的坐標(biāo)是(2,2),若點(diǎn)P在x軸上,且△APO是等腰三角形,則點(diǎn)P有_____個(gè).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,以△ABC的邊AB為直徑的⊙O分別交BC、AC于F、G,且G是![]() 的中點(diǎn),過點(diǎn)G作DE⊥BC,垂足為E,交BA的延長(zhǎng)線于點(diǎn)D
的中點(diǎn),過點(diǎn)G作DE⊥BC,垂足為E,交BA的延長(zhǎng)線于點(diǎn)D
(1)求證:DE是的⊙O切線;
(2)若AB=6,BG=4,求BE的長(zhǎng);
(3)若AB=6,CE=1.2,請(qǐng)直接寫出AD的長(zhǎng).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知,直線![]() 分別交
分別交![]() 軸
軸![]() 軸于
軸于![]() 、
、![]() 兩點(diǎn),
兩點(diǎn),![]() 、
、![]() 的長(zhǎng)滿足
的長(zhǎng)滿足![]() ,點(diǎn)
,點(diǎn)![]() 是直線
是直線![]() 上一點(diǎn),且
上一點(diǎn),且![]() .
.

![]() 求直線
求直線![]() 的解析式;
的解析式;
![]() 求過點(diǎn)
求過點(diǎn)![]() 的反比例函數(shù)解析式;
的反比例函數(shù)解析式;
![]() 點(diǎn)
點(diǎn)![]() 在反比例函數(shù)圖象上是否存在一點(diǎn)
在反比例函數(shù)圖象上是否存在一點(diǎn)![]() ,使以點(diǎn)
,使以點(diǎn)![]() 、
、![]() 、
、![]() 、
、![]() 為頂點(diǎn),
為頂點(diǎn),![]() 為腰的四邊形為梯形?若存在,請(qǐng)直接寫出點(diǎn)
為腰的四邊形為梯形?若存在,請(qǐng)直接寫出點(diǎn)![]() 的坐標(biāo);若不存在,請(qǐng)說明理由.
的坐標(biāo);若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
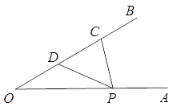
【題目】已知![]() ,點(diǎn)
,點(diǎn)![]() 為射線
為射線![]() 上一點(diǎn),點(diǎn)
上一點(diǎn),點(diǎn)![]() 為
為![]() 的中點(diǎn),且
的中點(diǎn),且![]() .當(dāng)點(diǎn)
.當(dāng)點(diǎn)![]() 在射線
在射線![]() 上運(yùn)動(dòng)時(shí) ,則
上運(yùn)動(dòng)時(shí) ,則![]() 與
與![]() 和的最小值為_______.
和的最小值為_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀下列材料,然后回答問題 .
已知 ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,….,當(dāng)
,….,當(dāng)![]() 為大于1的奇數(shù)時(shí),
為大于1的奇數(shù)時(shí),![]() ;當(dāng)
;當(dāng)![]() 為大于1的偶數(shù)時(shí),
為大于1的偶數(shù)時(shí),![]() .
.
(1)求![]() ;(用含
;(用含![]() 的代數(shù)式表示)
的代數(shù)式表示)
(2)直接寫出![]() ;(用含
;(用含![]() 的代數(shù)式表示)
的代數(shù)式表示)
(3)計(jì)算:![]() = .
= .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,是瑞安部分街道示意圖,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為“公交汽車”停靠點(diǎn),甲公共汽車從
為“公交汽車”停靠點(diǎn),甲公共汽車從![]() 站出發(fā),按照
站出發(fā),按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的順序到達(dá)
的順序到達(dá)![]() 站,乙公共汽車從
站,乙公共汽車從![]() 站出發(fā),按照
站出發(fā),按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的順序到達(dá)
的順序到達(dá)![]() 站,如果甲、乙兩車分別從
站,如果甲、乙兩車分別從![]() 、
、![]() 兩站同時(shí)出發(fā),各站耽誤的時(shí)間相同,兩輛車速度也一樣,則( )
兩站同時(shí)出發(fā),各站耽誤的時(shí)間相同,兩輛車速度也一樣,則( )
A. 甲車先到達(dá)指定站 B. 乙車先到達(dá)指定站
C. 同時(shí)到達(dá)指定站 D. 無法確定
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
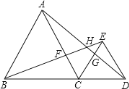
【題目】如圖,將△ABC分別沿AB,AC翻折得到△ABD 和△AEC,線段BD與AE交于點(diǎn) F,連接BE .
(1)如果∠ABC=16,∠ACB=30°,求∠DAE的度數(shù);
(2)如果BD⊥CE,求∠CAB 的度數(shù).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB="AC," AB+BC=8.將△ABC折疊,使得點(diǎn)A落在點(diǎn)B處,折痕DF分別與AB、AC交于點(diǎn)D、F,連接BF,則△BCF的周長(zhǎng)是( )
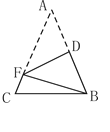
A.8B.16C.4D.10
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com