
【題目】如圖,∠ACL=90°,AC=4,動(dòng)點(diǎn)B在射線CL,CH⊥AB于點(diǎn)H,以H為圓心,HB為半徑作圓交射線BA于點(diǎn)D,交直線CD于點(diǎn)F,交直線BC于點(diǎn)E.設(shè)BC=m.

(1)當(dāng)∠A=30°時(shí),求∠CDB的度數(shù);
(2)當(dāng)m=2時(shí),求BE的長(zhǎng)度;
(3)在點(diǎn)B的整個(gè)運(yùn)動(dòng)過(guò)程中,
①當(dāng)BC=3CE時(shí),求出所有符合條件的m的值.
②連接EH,FH,當(dāng)tan∠FHE=![]() 時(shí),直接寫(xiě)出△FHD與△EFH面積比.
時(shí),直接寫(xiě)出△FHD與△EFH面積比.
【答案】(1)60°;(2)![]() ;(3)①m=2
;(3)①m=2![]() 或4
或4![]() ;②
;②![]()
【解析】
(1)根據(jù)題意由HB=HD,CH⊥BD可知:CH是BD的中垂線,再由∠A=30°得:∠CDB=∠ABC=60°;
(2)由題意可知當(dāng)m=2時(shí),由勾股定理可得:AB=2![]() ,cos∠ABC=
,cos∠ABC=![]() ,過(guò)點(diǎn)H作HK⊥BC于點(diǎn)K,利用垂徑定理可得結(jié)論;
,過(guò)點(diǎn)H作HK⊥BC于點(diǎn)K,利用垂徑定理可得結(jié)論;
(3))①要分兩種情況:I.當(dāng)點(diǎn)E在C右側(cè)時(shí),II.當(dāng)點(diǎn)E在C左側(cè)時(shí);根據(jù)相似三角形性質(zhì)和勾股定理即可求得結(jié)論;
②根據(jù)題意先證明EF∥BD,根據(jù)平行線間距離相等可得:△FHD與△EFH高相等,面積比等于底之比,再由tan∠FHE=![]() 可求得
可求得![]() 的值即可.
的值即可.
解:(1)∵∠A=30°,∠ACB=90°,
∴∠ABC=60°,
∵HB=HD,CH⊥BD,
∴CH是BD的中垂線,
∴CB=CD,
∴∠CDB=∠ABC=60°;
(2)如圖1,過(guò)點(diǎn)H作HK⊥BC于點(diǎn)K,

當(dāng)m=2時(shí),BC=2,
∴AB=![]() =2
=2![]() ,
,
∴cos∠ABC=![]() =
=![]() ,
,
∴BH=BCcos∠ABC=![]() ,
,
∴BK=BHcos∠ABC=![]() ,
,
∴BE=2BK=![]() ;
;
(3)①分兩種情況:
I.當(dāng)點(diǎn)E在C右側(cè)時(shí),如圖2,連結(jié)DE,由BD是直徑,得DE⊥BC,

∵BC=3CE=m,
∴CE=![]() m,BE=
m,BE=![]() m,
m,
∵DE∥AC,
∴△DEB~△ACB,
∴![]() =
=![]() =
=![]() ,
,
∴DE=![]() AC=
AC=![]() ,
,
∵CD=CB=m,
∴Rt△CDE中,由勾股定理得: =m2,
=m2,
∵m>0,
∴m=2![]() ;
;
II.當(dāng)點(diǎn)E在C左側(cè)時(shí),如圖3,連結(jié)DE,由BD是直徑,得DE⊥BC,

∵BC=3CE,
∴CE=![]() m,BE=
m,BE=![]() m,
m,
∵DE∥AC,
∴△DEB~△ACB,
∴![]() =
=![]() =
=![]() ,
,
∴DE=![]() AC=6,
AC=6,
∵CD=CB=m,
∴Rt△CDE中,由勾股定理得:62+ =m2,
=m2,
∵m>0,
∴m=4![]() ;
;
綜上所述,①當(dāng)BC=3CE時(shí),m=2![]() 或4
或4![]() .
.
②如圖4,過(guò)F作FG⊥HE于點(diǎn)G,

∵CH⊥AB,HB=HD,
∴CB=CD,
∴∠CBD=∠CDB,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴EF∥BD,
∴![]() =
=![]() ,
,
∵在Rt△FHG中,![]() =tan∠FHE=
=tan∠FHE=![]() ,
,
設(shè)FG=5k,HG=12k,則FH=![]() =
=![]() =13k,
=13k,
∴DH=HE=FH=13k,EG=HE﹣HG=13k﹣12k=k,
∴EF=![]() =
=![]() =
=![]() k,
k,
∴![]() =
=![]() =
=![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,下列網(wǎng)格由小正方形組成,點(diǎn)![]() 都在正方形網(wǎng)格的格點(diǎn)上.
都在正方形網(wǎng)格的格點(diǎn)上.
(1)在圖1中畫(huà)出一個(gè)以線段![]() 為邊,且與
為邊,且與![]() 面積相等但不全等的格點(diǎn)三角形;
面積相等但不全等的格點(diǎn)三角形;
(2)在圖2和圖3中分別畫(huà)出一個(gè)以線段![]() 為邊,且與
為邊,且與![]() 相似(但不全等)的格點(diǎn)三角形,并寫(xiě)出所畫(huà)三角形與
相似(但不全等)的格點(diǎn)三角形,并寫(xiě)出所畫(huà)三角形與![]() 的相似比.(相同的相似比算一種)
的相似比.(相同的相似比算一種)
(1)
(2)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,已知點(diǎn)A的坐標(biāo)是(4,0),并且OA=OC=4OB,動(dòng)點(diǎn)P在過(guò)A,B,C三點(diǎn)的拋物線上.
(1)求拋物線的解析式;
(2)在AC上方的拋物線上有一動(dòng)點(diǎn)G,如圖,當(dāng)點(diǎn)G運(yùn)動(dòng)到某位置時(shí),以AG,AO為鄰邊的平行四邊形第四個(gè)頂點(diǎn)恰好也在拋物線上,求出此時(shí)點(diǎn)G的坐標(biāo);
(3)若拋物線上存在點(diǎn)P,使得△ACP是以AC為直角邊的直角三角形,直接寫(xiě)出所有符合條件的點(diǎn)P的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,△ABC是⊙O的內(nèi)接三角形,AB是⊙O的直徑,OF⊥AB,交AC于點(diǎn)F,點(diǎn)E在AB的延長(zhǎng)線上,射線EM經(jīng)過(guò)點(diǎn)C,且∠ACE+∠AFO=180°.
(1)求證:EM是⊙O的切線;
(2)若∠A=∠E,BC=![]() ,求陰影部分的面積.(結(jié)果保留
,求陰影部分的面積.(結(jié)果保留![]() 和根號(hào)).
和根號(hào)).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為關(guān)注學(xué)生出行安全,調(diào)查了某班學(xué)生出行方式,調(diào)查結(jié)果分為四類(lèi):A﹣騎自行車(chē),B﹣步行,C﹣?zhàn)鐓^(qū)巴士,D﹣其它,并將調(diào)査結(jié)果繪制成以下兩幅不完整的統(tǒng)計(jì)圖.
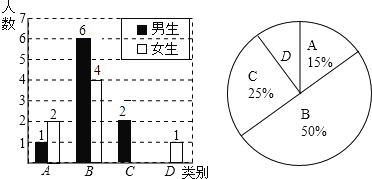
請(qǐng)你根據(jù)統(tǒng)計(jì)圖,解答下列問(wèn)題:
(1)本次一共調(diào)査了多少名學(xué)生?
(2)C類(lèi)女生有 名,D類(lèi)男生有 名,并將條形統(tǒng)計(jì)圖補(bǔ)充完整.
(3)若從被調(diào)查的A類(lèi)和D類(lèi)學(xué)生中分別隨機(jī)選取一位同學(xué)進(jìn)行進(jìn)一步調(diào)查,請(qǐng)用列表法或畫(huà)樹(shù)狀圖的方法求出所選同學(xué)中恰好是一位男同學(xué)和一位女同學(xué)的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公司共有![]() 三個(gè)部門(mén),根據(jù)每個(gè)部門(mén)的員工人數(shù)和相應(yīng)每人所創(chuàng)的年利潤(rùn)繪制成如下的統(tǒng)計(jì)表和扇形圖.
三個(gè)部門(mén),根據(jù)每個(gè)部門(mén)的員工人數(shù)和相應(yīng)每人所創(chuàng)的年利潤(rùn)繪制成如下的統(tǒng)計(jì)表和扇形圖.

各部門(mén)人數(shù)及每人所創(chuàng)年利潤(rùn)統(tǒng)計(jì)表
部門(mén) | 員工人數(shù) | 每人所創(chuàng)的年利潤(rùn)/萬(wàn)元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
(1)①在扇形圖中,C部門(mén)所對(duì)應(yīng)的圓心角的度數(shù)為_(kāi)__________;
②在統(tǒng)計(jì)表中,![]() ___________,
___________,![]() ___________;
___________;
(2)求這個(gè)公司平均每人所創(chuàng)年利潤(rùn).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】(6分)如圖,△ABC三個(gè)頂點(diǎn)的坐標(biāo)分別為A(2,4),B(1,1),C(4,3).

(1)請(qǐng)畫(huà)出△ABC關(guān)于x軸對(duì)稱的△A1B1C1,并寫(xiě)出點(diǎn)A1的坐標(biāo);
(2)請(qǐng)畫(huà)出△ABC繞點(diǎn)B逆時(shí)針旋轉(zhuǎn)90°后的△A2BC2;
(3)求出(2)中C點(diǎn)旋轉(zhuǎn)到C2點(diǎn)所經(jīng)過(guò)的路徑長(zhǎng)(記過(guò)保留根號(hào)和π).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】《九章算術(shù)》是我國(guó)古代數(shù)學(xué)的經(jīng)典著作,書(shū)中有一個(gè)問(wèn)題:“今有黃金九枚,白銀一十一枚,稱之重適等.交易其一,金輕十三兩.問(wèn)金、銀一枚各重幾何?”.意思是:甲袋中裝有黃金9枚(每枚黃金重量相同),乙袋中裝有白銀11枚(每枚白銀重量相同),稱重兩袋相等.兩袋互相交換1枚后,甲袋比乙袋輕了13兩(袋子重量忽略不計(jì)).問(wèn)黃金、白銀每枚各重多少兩?設(shè)每枚黃金重x兩,每枚白銀重y兩,根據(jù)題意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
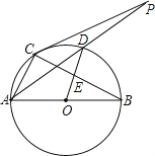
【題目】 如圖,圓O是以AB為直徑的△ABC的外接圓,D是劣弧![]() 的中點(diǎn),連AD并延長(zhǎng)與過(guò)C點(diǎn)的切線交于點(diǎn)P,OD與BC相交于E;
的中點(diǎn),連AD并延長(zhǎng)與過(guò)C點(diǎn)的切線交于點(diǎn)P,OD與BC相交于E;
(1)求證:OE=![]() AC;
AC;
(2)求證:![]() ;
;
(3)當(dāng)AC=6,AB=10時(shí),求切線PC的長(zhǎng).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com