
【題目】某家電銷售商城電冰箱的銷售價為每臺2100元,空調的銷售價為每臺1750元,每臺電冰箱的進價比每臺空調的進價多400元,商城用80000元購進電冰箱的數量與用64000元購進空調的數量相等.
(1)求每臺電冰箱與空調的進價分別是多少;
(2)現在商城準備一次購進這兩種家電共100臺,設購進電冰箱x臺,這100臺家電的銷售總利潤為y元,要求購進空調數量不超過電冰箱數量的2倍,總利潤不低于13000元,請分析合理的方案共有多少種,并確定獲利最大的方案以及最大利潤;
(3)實際進貨時,廠家對電冰箱出廠價下調k(0<k<100)元,若商店保持這兩種家電的售價不變,請你根據以上信息及(2)問中條件,設計出使這100臺家電銷售總利潤最大的進貨方案.
【答案】(1)1600,2000;(2)有7種,當購進電冰箱34臺,空調66臺獲利最大,最大利潤為13300元;(3)當50<k<100時,購進電冰箱40臺,空調60臺銷售總利潤最大;當0<k<50時,購進電冰箱34臺,空調66臺銷售總利潤最大;當k=50時,每種進貨方案的總利潤都一樣.
【解析】
(1)設每臺空調的進價為x元,則每臺電冰箱的進價為(x+400)元,根據“商城用80000元購進電冰箱的數量與用64000元購進空調的數量相等”,列出方程,即可解答;
(2)設購進電冰箱x臺,這100臺家電的銷售總利潤為y元,表示出總利潤y=﹣50x+15000,根據題意得:求出x的取值范圍,根據x為正整數,所以x=34,35,36,37,38,39,40,即合理的方案共有7種,利用一次函數的性質,確定獲利最大的方案以及最大利潤;
(3)當電冰箱出廠價下調k(0<k<100)元時,則利潤y=(k﹣50)x+15000,分兩種情況討論:當k﹣50>0;當k﹣50<0;利用一次函數的性質,即可解答.
解:(1)設每臺空調的進價為x元,則每臺電冰箱的進價為(x+400)元,根據題意得:
![]() ,解得:x=1600,
,解得:x=1600,
經檢驗,x=1600是原方程的解,x+400=1600+400=2000,
答:每臺空調的進價為1600元,則每臺電冰箱的進價為2000元.
(2)設購進電冰箱x臺,這100臺家電的銷售總利潤為y元,
則y=(2100﹣2000)x+(1750﹣1600)(100﹣x)=﹣50x+15000,根據題意得:
![]() ,解得:
,解得:![]() ,
,
∵x為正整數,∴x=34,35,36,37,38,39,40,
∴合理的方案共有7種,即①電冰箱34臺,空調66臺;②電冰箱35臺,空調65臺;③電冰箱36臺,空調64臺;④電冰箱37臺,空調63臺;⑤電冰箱38臺,空調62臺;⑥電冰箱39臺,空調61臺;⑦電冰箱40臺,空調60臺;
∵y=﹣50x+15000,k=﹣50<0,∴y隨x的增大而減小,
∴當x=34時,y有最大值,最大值為:﹣50×34+15000=13300(元),
答:當購進電冰箱34臺,空調66臺獲利最大,最大利潤為13300元.
(3)當廠家對電冰箱出廠價下調k(0<k<100)元,若商店保持這兩種家電的售價不變,
則利潤y=(2100﹣2000+k)x+(1750﹣1600)(100﹣x)=(k﹣50)x+15000,
當k﹣50>0,即50<k<100時,y隨x的增大而增大,
∵![]() ,
,
∴當x=40時,這100臺家電銷售總利潤最大,即購進電冰箱40臺,空調60臺;
當k﹣50<0,即0<k<50時,y隨x的增大而減小,
∵![]() ,
,
∴當x=34時,這100臺家電銷售總利潤最大,即購進電冰箱34臺,空調66臺;
答:當50<k<100時,購進電冰箱40臺,空調60臺銷售總利潤最大;當0<k<50時,購進電冰箱34臺,空調66臺銷售總利潤最大.


 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案科目:初中數學 來源: 題型:
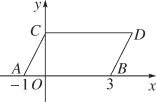
【題目】如圖,在平面直角坐標系中,點A,B的坐標分別為(-1,0),(3,0),現同時將A,B兩點向右平移1個單位,再向上平移2個單位,分別得到點A,B的對應點C,D,連接AC,BD,CD.
(1)求點C,D的坐標;
(2)若點P在直線BD上運動,連接PC,PO.
①若點P在線段BD上(不與B,D重合)時,求S△CDP+S△BOP的取值范圍;
②若點P在直線BD上運動,試探索∠CPO,∠DCP,∠BOP的關系,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一個單位為1的方格紙上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜邊在x軸上、斜邊長分別為2,4,6,…的等腰直角三角形.若△A1A2A3的頂點坐標分別為A1(2,0),A2(1,-1),A3(0,0),則依圖中所示規律,A2017的橫坐標為( )

A. 1010 B. 2 C. 1 D. ﹣1006
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們已經知道(a﹣b)2≥0,即a2﹣2ab+b2≥0.所以a2+b2≥2ab(當且僅當a=b時取等號).
閱讀1:若a、b為實數,且a>0,b>0.
∵(![]() )2≥0,∴a﹣2
)2≥0,∴a﹣2![]() +b≥0,∴a+b≥2
+b≥0,∴a+b≥2![]() (當且僅當a=b時取等號).
(當且僅當a=b時取等號).
閱讀2:若函數y=x![]() (m>0,x>0,m為常數).由閱讀1結論可知:x
(m>0,x>0,m為常數).由閱讀1結論可知:x![]() 即x
即x![]() ∴當x
∴當x![]() 即x2=m,∴x=
即x2=m,∴x=![]() (m>0)時,函數y=x
(m>0)時,函數y=x![]() 的最小值為2
的最小值為2![]() .
.
閱讀理解上述內容,解答下列問題:
問題1:當x>0時,![]() 的最小值為 ;當x<0時,
的最小值為 ;當x<0時,![]() 的最大值為 .
的最大值為 .
問題2:函數y=a+![]() (a>1)的最小值為 .
(a>1)的最小值為 .
問題3:求代數式![]() (m>﹣2)的最小值,并求出此時的m的值.
(m>﹣2)的最小值,并求出此時的m的值.
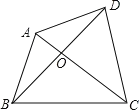
問題4:如圖,四邊形ABCD的對角線AC,BD相交于點O,△AOB、△COD的面積分別為4和16,求四邊形ABCD面積的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
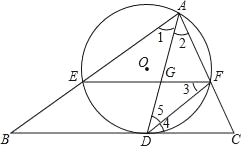
【題目】如圖,AD是△ABC的角平分線,以AD為弦的⊙O交AB、AC于E、F,已知EF∥BC.
(1)求證:BC是⊙O的切線;
(2)若已知AE=9,CF=4,求DE長;
(3)在(2)的條件下,若∠BAC=60°,求tan∠AFE的值及GD長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將二次函數y=x2-m(其中m>0)的圖象在x軸下方的部分沿x軸翻折,圖象的其余部分保持不變,形成新的圖象記為y1,另有一次函數y=x+b的圖象記為y2,則以下說法:
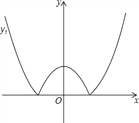
①當m=1,且y1與y2恰好有三個交點時b有唯一值為1;
②當b=2,且y1與y2恰有兩個交點時,m>4或0<m<![]() ;
;
③當m=-b時,y1與y2一定有交點;
④當m=b時,y1與y2至少有2個交點,且其中一個為(0,m).
其中正確說法的序號為 ______ .
查看答案和解析>>
科目:初中數學 來源: 題型:
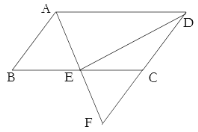
【題目】如圖,平行四邊形ABCD中,AD=2AB,E是BC的中點,連結AE并延長交DC的延長線于點F.
(1)求證:DE⊥AF;
(2)若∠B=60°,DE=4,求AB的長,
查看答案和解析>>
科目:初中數學 來源: 題型:
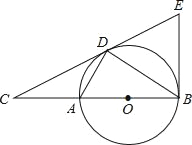
【題目】如圖,點D為⊙O上一點,點C在直徑BA的延長線上,且∠CDA=∠CBD.(1)判斷直線CD和⊙O的位置關系,并說明理由.
(2)過點B作⊙O的切線BE交直線CD于點E,若AC=2,⊙O的半徑是3,求∠BEC的正切值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知線段![]() ,
, ![]() 于點
于點![]() ,且
,且![]() ,
, ![]() 是射線
是射線![]() 上一動點,
上一動點, ![]() 、
、![]() 分別是
分別是![]() ,
, ![]() 的中點,過點
的中點,過點![]() ,
, ![]() ,
, ![]() 的圓與
的圓與![]() 的另一交點
的另一交點![]() (點
(點![]() 在線段
在線段![]() 上),連結
上),連結![]() ,
, ![]() .
.

(![]() )當
)當![]() 時,則
時,則![]() 的度數為__________.
的度數為__________.
(![]() )在點
)在點![]() 的運動過程中,當
的運動過程中,當![]() 時,取四邊形
時,取四邊形![]() 一邊的兩端點和線段
一邊的兩端點和線段![]() 上一點
上一點![]() ,若以這三點為頂點的三角形是直角三角形,當
,若以這三點為頂點的三角形是直角三角形,當![]() 時,則
時,則![]() 的值為__________.
的值為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com