
【題目】△OAB在第一象限中,OA=AB,OA⊥AB,O是坐標原點,且函數y=![]() 正好過A,B兩點,BE⊥x軸于E點,則OE2﹣BE2的值為( )
正好過A,B兩點,BE⊥x軸于E點,則OE2﹣BE2的值為( )
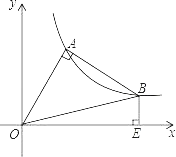
A. 3B. 2C. 3D. 4
【答案】D
【解析】
過點A作AF⊥y軸于點F,延長EB交FA的延長線于點D.由題意可證四邊形DEOF是矩形,可得DE=OF,DF=OE,由題意可證△AFO≌△BDA,可得AF=DB, AD=OF,設出A點坐標,表示出BE與OE,即可求出所求式子的值.
如圖:過點A作AF⊥y軸于點F,延長EB交FA的延長線于點D.
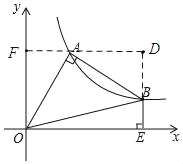
∵AF⊥OF,BE⊥OE,OE⊥OF
∴四邊形DEOF是矩形
∴∠D=90°,OF=DE,DF=OE
設點A(a,![]() ),即AF=a,OF=
),即AF=a,OF=![]()
∵∠BAO=90°,AF⊥FO
∴∠BAD+∠FAO=90°,∠FAO+∠FOA=90°
∴∠DAB=∠AOF且AO=AB,∠AFO=∠ADB=90°
∴△AFO≌△BDA(AAS)
∴AD=OF=![]() ,DB=AF=a
,DB=AF=a
∴BE=DE﹣DB=![]() ﹣a,OE=DF=AF+AD=a+
﹣a,OE=DF=AF+AD=a+![]()
∴OE2﹣BE2=(a+![]() )2﹣(
)2﹣(![]() ﹣a)2=4
﹣a)2=4
故選:D.


 小學數學口算題卡脫口而出系列答案
小學數學口算題卡脫口而出系列答案 優秀生應用題卡口算天天練系列答案
優秀生應用題卡口算天天練系列答案 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線y=![]() x+6與x、y軸分別交于點A,點B,雙曲線的解析式為
x+6與x、y軸分別交于點A,點B,雙曲線的解析式為![]()

(1)求出線段AB的長
(2)在雙曲線第四象限的分支上存在一點C,使得CB⊥AB,且CB=AB,求k的值;
(3)在(1)(2)的條件下,連接AC,點D為BC的中點,過D作AC的垂線BF,交AC于B,交直線AB于F,連AD,若點P為射線AD上的一動點,連接PC、PF,當點P在射線AD上運動時,PF![]() -PC
-PC![]() 的值是否發生改變?若改變,請求出其范圍;若不變,請證明并求出定值。
的值是否發生改變?若改變,請求出其范圍;若不變,請證明并求出定值。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,拋物線y=ax2+bx+c經過點A(﹣2,0)、B(4,0)、C(0,3)三點.
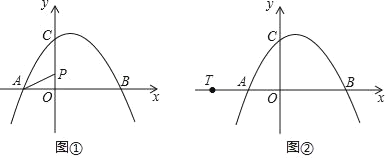
(1)試求拋物線的解析式;
(2)點P是y軸上的一個動點,連接PA,試求5PA+4PC的最小值;
(3)如圖②,若直線l經過點T(﹣4,0),Q為直線l上的動點,當以A、B、Q為頂點所作的直角三角形有且僅有三個時,試求直線l的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知梯形ABCD中,AD∥BC,AB=AC,E是邊BC上的點,且∠AED=∠CAD,DE交AC于點F.
(1)求證:△ABE∽△DAF;
(2)當ACFC=AEEC時,求證:AD=BE.

查看答案和解析>>
科目:初中數學 來源: 題型:
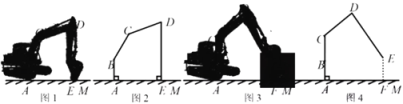
【題目】某挖掘機的底座高AB=0.8米,動臂BC=1.2米,CD=1.5米,BC與CD的固定夾角∠BCD=140°.初始位置如圖1,斗桿頂點D與鏟斗頂點E所在直線DE垂直地面AM于點E,測得∠CDE=70°(示意圖2).工作時如圖3,動臂BC會繞點B轉動,當點A,B,C在同一直線時,斗桿頂點D升至最高點(示意圖4).
(1)求挖掘機在初始位置時動臂BC與AB的夾角∠ABC的度數.
(2)問斗桿頂點D的最高點比初始位置高了多少米(精確到0.1米)?
(考數據:sin50°≈0.77,cos50°≈0.64,sin70°≈0.94,cos70°≈0.34,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A(3,0),B(0,-1),連接AB,過B點作AB的垂線段,使BA=BC,連接AC.
(1)如圖1,求C點坐標;
(2)如圖2,若P點從A點出發,沿x軸向左平移,連接BP,作等腰直角三角形△BPQ,連接CQ.求證:PA=CQ.
(3)在(2)的條件下,若C、P、Q三點共線,求此時P點坐標及∠APB的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一艘輪船航行到 B 處時,測得小島 A 在船的北偏東 60°的方向,輪船從 B 處繼續向正東方向航行 20 海里到達 C 處時,測得小島 A 在北船的北偏東 30°的方向.
(1)若小島 A 到這艘輪船航行路線 BC 的距離是 AD,求 AD 的長.
(2)已知在小島周圍 17 海里內有暗礁,若輪船不改變航向繼續向前行駛,試問輪船有無觸礁的危險?(![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中數學 來源: 題型:
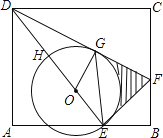
【題目】如圖,E是長方形ABCD的邊AB上的點,EF⊥DE交BC于點F
(1)求證:△ADE∽△BEF;
(2)設H是ED上一點,以EH為直徑作⊙O,DF與⊙O相切于點G,若DH=OH=3,求圖中陰影部分的面積(結果保留到小數點后面第一位,![]() ≈1.73,π≈3.14).
≈1.73,π≈3.14).
查看答案和解析>>
科目:初中數學 來源: 題型:
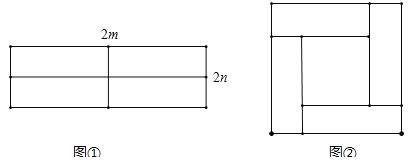
【題目】如圖,圖①所示是一個長為2m,寬為2n的長方形,用剪刀均分成四個小長方形,然后按圖②的方式拼成一個大正方形.
(1)圖②中的大正方形的邊長等于 ,圖②中的小正方形的邊長等于 ;
(2)圖②中的大正方形的面積等于 ,圖②中的小正方形的面積等于 ;圖①中每個小長方形的面積是 ;
(3)觀察圖②,你能寫出(m+n)2,(m﹣n)2,mn這三個代數式間的等量關系嗎? .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com