
【題目】如圖,將Rt△ABC沿BC所在直線平移得到△DEF.
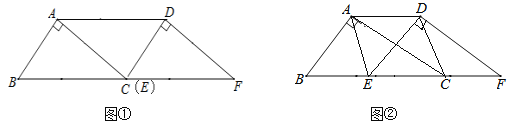
(1)如圖①,當點E移動到點C處時,連接AD,求證:△CDA≌△ABC;
(2)如圖②,當點E移動到BC中點時,連接AD、AE、CD,請你判斷四邊形AECD的形狀,并說明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
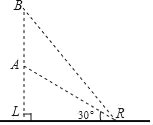
【題目】如圖所示,運載火箭從地面L處垂直向上發射,當火箭到達A點時,從位于地面R處的雷達測得AR的距離是40km,仰角是30°,n秒后,火箭到達B點,此時仰角是45°,則火箭在這n秒中上升的高度是_____km.
查看答案和解析>>
科目:初中數學 來源: 題型:
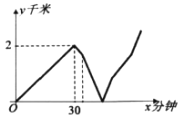
【題目】周末小明勻速步行趕往學校參加學校組織的植樹活動,小明從家出發30分鐘后,忽然想起沒有帶植樹工具,于是馬上掉頭往回走行走速度比之前提高了1千米/時(仍保持勻速步行),同時小明打電話給爸爸,請爸爸幫他把植樹工具送過來,從小明開始打電話到爸爸出門一共用了4分鐘,爸爸的行走速度與此時小明的行走速度相同,兩人相遇后,小明立即趕往學校,爸爸則轉身回家,兩人速度均保持不變,爸爸在回家途中用了10分鐘吃早餐,然后立即回家,當爸爸到家時小明剛好到達學校.爸爸和小明相距的路程y(千米)與小明從家出發的時間x(分鐘)之間的關系如圖所示,求今天早上小明從家到學校途中行走的總路程是________千米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,經過![]() 和
和![]() 兩點的拋物線
兩點的拋物線![]() 交
交![]() 軸于
軸于![]() 兩點,
兩點,![]() 是拋物線上一動點,平行于
是拋物線上一動點,平行于![]() 軸的直線
軸的直線![]() 經過點
經過點![]() .
.
(1)求拋物線的解析式;
(2)如圖1,![]() 軸上有點
軸上有點![]() 連接
連接![]() ,設點
,設點![]() 到直線
到直線![]() 的距離為
的距離為![]() .
.![]() .小明在探究
.小明在探究![]() 的值的過程中,是這樣思考的:當
的值的過程中,是這樣思考的:當![]() 是拋物線的頂點時,計算
是拋物線的頂點時,計算![]() 的值;當
的值;當![]() 不是拋物線的頂點時,猜想
不是拋物線的頂點時,猜想![]() 是一個定值.請你直接寫出
是一個定值.請你直接寫出![]() 的值,并證明小明的猜想.
的值,并證明小明的猜想.
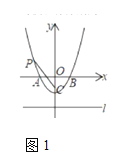
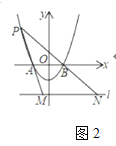
(3)如圖2,點![]() 在第二象限,分別連接
在第二象限,分別連接![]() 、
、![]() ,并延長交直線
,并延長交直線![]() 于
于![]() 兩點.若
兩點.若![]() 兩點的橫坐標分別為
兩點的橫坐標分別為![]() ,試探究
,試探究![]() 之間的數量關系.
之間的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB=16cm,AC=12cm,動點P、Q分別以每秒2cm和1cm的速度同時開始運動,其中點P從點A出發,沿AC邊一直移到點C為止,點Q從點B出發沿BA邊一直移到點A為止,(點P到達點C后,點Q繼續運動)
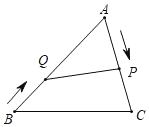
(1)請直接用含t的代數式表示AP的長和AQ的長,并寫出定義域.
(2)當t等于何值時,△APQ與△ABC相似?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,正方形ABCD的頂點分別為A(0,1),B(-1,0),C(0,-1),D(1,0).對于圖形M,給出如下定義:P為圖形M上任意一點,Q為正方形ABCD邊上任意一點,如果P,Q兩點間的距離有最大值,那么稱這個最大值為圖形M的“正方距”,記作d(M).
(1)已知點E(0,4),
①直接寫出d(點E)的值;
②直線y=kx+4(k≠0)與x軸交于點F,當d(線段EF)取最小值時,求k的取值范圍;
(2)⊙T的圓心為T(7,t),半徑為1.若d(⊙T)<11,請直接寫出t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】鐘南山院士談到防護新型冠狀病毒肺炎時說:“我們需要重視防護,但也不必恐慌,盡量少去人員密集的場所,出門戴口罩,在室內注意通風,勤洗手,多運動,少熬夜.”某社區為了加強社區居民對新型冠狀病毒肺炎防護知識的了解,通過微信群宣傳新型冠狀病毒肺炎的防護知識,并鼓勵社區居民在線參與作答《![]() 年新型冠狀病毒防治全國統一考試(全國卷)》試卷(滿分
年新型冠狀病毒防治全國統一考試(全國卷)》試卷(滿分![]() 分),社區管理員隨機從有
分),社區管理員隨機從有![]() 人的某小區抽取若干名人員的答卷成績,并對他們的成績(單位:分)統計整理后繪制了一幅不完整的統計表(如圖所示)
人的某小區抽取若干名人員的答卷成績,并對他們的成績(單位:分)統計整理后繪制了一幅不完整的統計表(如圖所示)
等級 | 成績( | 頻數 | 頻率 |
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
合計 |
|
| |
根據上面提供的信息,回答下列問題:
(1)統計表中的![]() =___,
=___,![]() =_____;
=_____;
(2)根據抽樣調查結果,請估計該小區答題成績為“![]() 級”的有多少人?
級”的有多少人?
(3)該社區有![]() 名男管理員和
名男管理員和![]() 名女管理員,現從中隨機挑選
名女管理員,現從中隨機挑選![]() 名管理員參加“社區防控”宣傳活動,請用樹狀圖法或列表法求出恰好選中“
名管理員參加“社區防控”宣傳活動,請用樹狀圖法或列表法求出恰好選中“![]() 男
男![]() 女”的概率.
女”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一方有難,八方支援. 在湖北武漢新冠肺炎疫情爆發期間,我市甲、乙兩所醫院分別有一男一女共4名醫護人員參與了支援湖北武漢抗擊疫情的任務.
(1)若從甲、乙兩醫院的援鄂醫護人員中分別隨機選1名,則所選的2名醫護人員性別相同的概率是 ;
(2)若從援鄂的4名醫護人員中隨機選2名,用列表或畫樹狀圖的方法求出這2名醫護人員來自同一所醫院的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A(-2,a),C(3a-10,1)是反比例函數![]() (x<0)圖象上的兩點.
(x<0)圖象上的兩點.
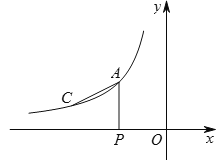
(1)求m的值;
(2)過點A作AP⊥x軸于點P,若直線y=kx+b經過點A,且與x軸交于點B,當∠PAC=∠PAB時,求直線AB的解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com