
【題目】如圖,在平行四邊形ABCD中,對角線AC、BD相交于點O,E、F是對角線AC上的兩點,當E、F滿足下列哪個條件時,四邊形DEBF不一定是平行四邊形的是( )
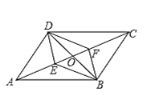
A. AE=CFB. DE=BF
C. ∠ADE=∠CBFD. ∠ABE=∠CDF
【答案】B
【解析】
若是四邊形的對角線互相平分,可證明這個四邊形是平行四邊形,選項A,C,D都能證明對角線互相平分,只有B不可以,由此即可得答案.
∵四邊形ABCD是平行四邊形,
∴AO=CO,BO=DO,AD//BC,AB//CD, AD=BC,AB=CD,
∴∠DAE=∠BCF,∠BAE=∠DCF,
A、∵AE=CF,
∴EO=FO,
∵DO=BO,
∴四邊形DEBF是平行四邊形;
C、∵∠ADE=∠CBF,AD=BC,∠DAE=∠BCF,
∴△ADE≌△CBF,
∴AE=CF,
∴EO=FO,
∵DO=BO,
∴四邊形DEBF是平行四邊形.
同理若∠ABE=∠CDF,也能證明△ABE≌△CDF,從而四邊形DEBF是平行四邊形;
只有B選項不能得出結論,
故選B.


科目:初中數學 來源: 題型:
【題目】為了解同學對體育活動的喜愛情況,某校設計了“你最喜歡的體育活動是哪一項(僅限一項)”的調查問卷.該校對本校學生進行隨機抽樣調查,以下是根據調查數據得到的統計圖的一部分.請根據以上信息解答以下問題:
(1)該校對多少名學生進行了抽樣調查?
(2)請補全圖1并標上數據.
(3)若該校共有學生900人,請你估計該校最喜歡跳繩項目的學生約有多少人?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一副三角板如圖擺放,點F是 45°角三角板△ABC的斜邊的中點,AC=4.當 30°角三角板DEF的直角頂點繞著點F旋轉時,直角邊DF,EF分別與AC,BC相交于點 M, N.在旋轉過程中有以下結論:①MF=NF;②CF與MN可能相等嗎;③MN 長度的最小值為 2;④四邊形CMFN的面積保持不變; ⑤△CMN面積的最大值為 2.其中正確的個數是_________.(填寫序號).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校“體育課外活動興趣小組”,開設了以下體育課外活動項目:A.足球 B.乒乓球C.羽毛球 D.籃球,為了解學生最喜歡哪一種活動項目,隨機抽取了部分學生進行調查,并將調查結果繪制成了兩幅不完整的統計圖,請回答下列問題:
(1)這次被調查的學生共有 人,在扇形統計圖中“D”對應的圓心角的度數為 ;
(2)請你將條形統計圖補充完整;
(3)在平時的乒乓球項目訓練中,甲、乙、丙、丁四人表現優秀,現決定從這四名同學中任選兩名參加市里組織的乒乓球比賽,求恰好選中甲、乙兩位同學的概率(用樹狀圖或列表法解答).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,五邊形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,則∠BAE的度數為何?( )

A. 115 B. 120 C. 125 D. 130
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】己知:如圖,E、F分別是ABCD的AD、BC邊上的點,且AE=CF.

(1)求證:△ABE≌△CDF;
(2)若M、N分別是BE、DF的中點,連接MF、EN,試判斷四邊形MFNE是怎樣的四邊形,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為提高飲水質量,越來越多的居民選購家用凈水器.我市飛龍商場抓住商機,從廠家購進了A、B兩種型號家用凈水器共100臺,A型號家用凈水器進價是150元/臺,B型號家用凈水器進價是250元/臺,購進兩種型號的家用凈水器共用去19000 元.
(1)求A、B兩種型號家用凈水器各購進了多少臺;
(2)為使每臺B型號家用凈水器的毛利潤是A型號的2倍,且保證售完這100臺家用凈水器的毛利潤不低于5600元,求每臺A型號家用凈水器的售價至少是多少元? (注: 毛利潤=售價一進價) .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知:∠MON=30°,點A1、A2、A3 在射線ON上,點B1、B2、B3…在射線OM上,△A1B1A2、△A2B2A3、△A3B3A4…均為等邊三角形,若OA1=a,則△A6B6A7的邊長為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
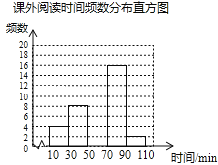
【題目】某學校為了解學生的課外閱讀情況,隨機抽取了50名學生,并統計他們平均每天的課外閱讀時間t(單位:min),然后利用所得數據繪制成如下不完整的統計表.
課外閱讀時間t | 頻數 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合計 | 50 | 100% |
請根據圖表中提供的信息回答下列問題:
(1)a= ,b= ;
(2)將頻數分布直方圖補充完整;
(3)若全校有900名學生,估計該校有多少學生平均每天的課外閱讀時間不少于50min?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com