
【題目】某商場準備進一批兩種不同型號的衣服,已知購進![]() 種型號衣服9件,
種型號衣服9件,![]() 種型號衣服10件,則共需1810元;若購進
種型號衣服10件,則共需1810元;若購進![]() 種型號衣服12件,
種型號衣服12件,![]() 種型號衣服8件,共需1880元;已知銷售一件
種型號衣服8件,共需1880元;已知銷售一件![]() 型號衣服可獲利18元,銷售一件
型號衣服可獲利18元,銷售一件![]() 型號衣服可獲利30元.要使在這次銷售中獲利不少于699元,且
型號衣服可獲利30元.要使在這次銷售中獲利不少于699元,且![]() 型號衣服不多于28件.
型號衣服不多于28件.
(1)求![]() 型號衣服進價各是多少元?
型號衣服進價各是多少元?
(2)若已知購進![]() 型號衣服是
型號衣服是![]() 型號衣服的2倍還多4件,則商店在這次進貨中可有幾種方案?并簡述購貨方案.
型號衣服的2倍還多4件,則商店在這次進貨中可有幾種方案?并簡述購貨方案.
【答案】(1)![]() 型號衣服每件90元,
型號衣服每件90元,![]() 型號衣服每件100元;(2)有三種進貨方案:①
型號衣服每件100元;(2)有三種進貨方案:① ![]() 型號衣服購買10件,
型號衣服購買10件,![]() 型號衣服購進24件;②
型號衣服購進24件;②![]() 型號衣服購買11件,
型號衣服購買11件,![]() 型號衣服購進26件;③
型號衣服購進26件;③![]() 型號衣服購買12件,
型號衣服購買12件,![]() 型號衣服購進28件.
型號衣服購進28件.
【解析】
(1)等量關系為:A種型號衣服9件×進價+B種型號衣服10件×進價=1810,A種型號衣服12件×進價+B種型號衣服8件×進價=1880;
(2)關鍵描述語是:獲利不少于699元,且A型號衣服不多于28件.關系式為:18×A型件數+30×B型件數≥699,A型號衣服件數≤28.
(1)設![]() 型號衣服每件
型號衣服每件![]() 元,
元,![]() 型號衣服每件
型號衣服每件![]() 元,
元,
則:![]() 解得
解得![]()
答:![]() 型號衣服每件90元,
型號衣服每件90元,![]() 型號衣服每件100元
型號衣服每件100元
(2)設![]() 型號衣服購進
型號衣服購進![]() 件,則
件,則![]() 型號衣服購進
型號衣服購進![]() 件,
件,
則: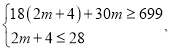 解得
解得![]()
![]() 為正整數,
為正整數,
![]() 、11、12,
、11、12,![]() 24、26、28.
24、26、28.
答:有三種進貨方案:
①![]() 型號衣服購買10件,
型號衣服購買10件,![]() 型號衣服購進24件;
型號衣服購進24件;
②![]() 型號衣服購買11件,
型號衣服購買11件,![]() 型號衣服購進26件;
型號衣服購進26件;
③ ![]() 型號衣服購買12件,
型號衣服購買12件,![]() 型號衣服購進28件.
型號衣服購進28件.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源: 題型:
【題目】英國《![]() ?》雜志最近對30部手機進行了檢測,結果發現有近四分之一的手機攜帶的細菌數量達到可接受數量的10倍,其中一部最臟的手機一度讓它的主人出現嚴重消化不良.在手機上發現的有害細菌中,最為常見的有害細菌當屬金黃色葡萄球菌.這種細菌可導致一系列感染,金黃色葡萄球菌為球形,直徑
?》雜志最近對30部手機進行了檢測,結果發現有近四分之一的手機攜帶的細菌數量達到可接受數量的10倍,其中一部最臟的手機一度讓它的主人出現嚴重消化不良.在手機上發現的有害細菌中,最為常見的有害細菌當屬金黃色葡萄球菌.這種細菌可導致一系列感染,金黃色葡萄球菌為球形,直徑![]() 左右,0.0000008米這個數用科學記數法表示為( )
左右,0.0000008米這個數用科學記數法表示為( )
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中考體育測試前,某區教育局為了了解選報引體向上的初三男生的成績情況,隨機抽測了本區部分選報引體向上項目的初三男生的成績,并將測試得到的成績繪成了下面兩幅不完整的統計圖:
請你根據圖中的信息,解答下列問題:
(![]() )寫出扇形圖中
)寫出扇形圖中![]() __________
__________![]() ,并補全條形圖.
,并補全條形圖.
(![]() )在這次抽測中,測試成績的眾數和中位數分別是__________個、__________個.
)在這次抽測中,測試成績的眾數和中位數分別是__________個、__________個.
(![]() )該區體育中考選報引體向上的男生共有
)該區體育中考選報引體向上的男生共有![]() 人,如果體育中考引體向上達
人,如果體育中考引體向上達![]() 個以上(含
個以上(含![]() 個)得滿分,請你估計該區體育中考中選報引體向上的男生能獲得滿分的有多少名?
個)得滿分,請你估計該區體育中考中選報引體向上的男生能獲得滿分的有多少名?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2﹣x+4與x軸交于點A,B,B點的坐標為(﹣4,0),與y軸交于點C.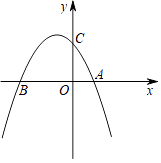
(1)求拋物線的解析式和對稱軸.
(2)連接AC、BC,在x軸下方的拋物線上求一點M,使△ABM與△ABC的面積相等.
(3)在x軸下方作平行于x軸的直線l,與拋物線交于點D、E兩點(點D在對稱軸的左側).過點D、E分別作x軸的垂線,垂足分別為G、F,當矩形DEFG中DE=2DG時,求D點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】知識鏈接:將兩個含30°角的全等三角尺放在一起,讓兩個30°角合在一起成60°,經過拼湊、觀察、思考,探究出“直角三角形中30°角所對的直角邊等于斜邊的一半”結論.
如圖:等邊三角形ABC的邊長為4cm,點D從點C出發沿CA向A運動,點E從B出發沿AB的延長線BF向右運動,已知點D、E都以每秒0.5cm的速度同時開始運動,運動過程中DE與BC相交于點P,設運動時間為x秒.
(1)請直接寫出AD長.(用x的代數式表示)
(2)當△ADE為直角三角形時,運動時間為幾秒?
(2)求證:在運動過程中,點P始終為線段DE的中點.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了了解七年級學生課外活動情況,隨機調查了該校若干名學生,調查他們喜歡各類課外活動的情況(課外活動分為四類:A﹣﹣喜歡打乒乓球的人,B﹣﹣喜歡踢足球的人,C﹣﹣喜歡打籃球的人,D﹣﹣喜歡其他的人),并將調查結果繪制成如下兩幅不完整的統計圖.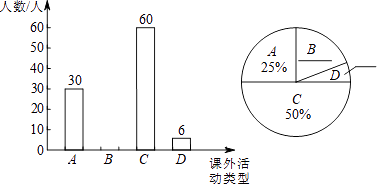
根據統計圖信息完成下列問題:
(1)調查的學生人數為人.
(2)補全條形統計圖和扇形統計圖.
(3)若該校七年級共有600人,請估計七年級學生中喜歡打乒乓球的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題探究
(1)請在圖①的正方形ABCD的對角線BD上作一點P,使PA+PC最小;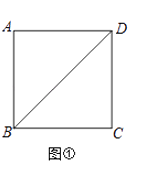
(2)如圖②,點P為矩形ABCD的對角線BD上一動點,AB=2,BC=2 ![]() ,點E為BC邊的中點,求作一點P,使PE+PC最小,并求這個最小值.
,點E為BC邊的中點,求作一點P,使PE+PC最小,并求這個最小值.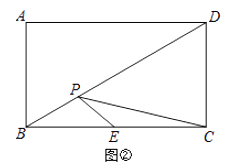
(3)如圖③,李師傅有一塊邊長為1000米的菱形ABCD采摘園,AC=1200米,BD為小路,BC的中點E為一水池,李師傅現在準備在小路BD上建一個游客臨時休息納涼室P,為了節省土地,使休息納涼室P到水池E與大門C的距離之和最短,那么是否存在符合條件的點P?若存在,請作出的點P位置,并求出這個最短距離;若不存在,請說明理由.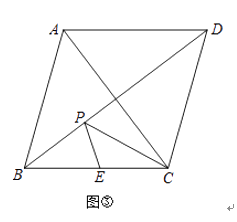
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com