【題目】如圖，在平行四邊形ABCD中，點E.F分別在AB、CD上，AE=CF，連接AF，BF，DE，CE，分別交于H、G.
求證：(1)四邊形AECF是平行四邊形。(2)EF與GH互相平分。
【答案】見解析
【解析】
(1)根據四邊形ABCD是平行四邊形,由平行四邊形的性質可得:
,
,
根據
,利用平行四邊形的判定定理可得:四邊形AECF是平行四邊形,
由
得四邊形AECF是平行四邊形,根據平行四邊形的性質可得:
,
根據,,,可得:
,
,根據平行四邊形的判定定理可得:四邊形BFDE是平行四邊形,再根據平行四邊形的性質可得:
,根據平行四邊形的判定定理可得:四邊形EGFH是平行四邊形,由平行四邊形的性質可得:
與GH互相平分.
四邊形ABCD是平行四邊形,
,,
,
四邊形AECF是平行四邊形,
由得:四邊形AECF是平行四邊形,
,
,,,
,,
四邊形BFDE是平行四邊形,
,
四邊形EGFH是平行四邊形,
與GH互相平分.
科目：初中數學 來源： 題型：
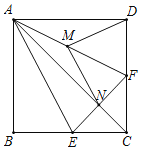
【題目】操作與證明：如圖，把一個含
角的直角三角板ECF和一個正方形ABCD擺放在一起，使三角板的直角頂點和正方形的頂點C重合，點E、F分別在正方形的邊CB、CD上，連接AC、AE、
其中AC與EF交于點N，取AF中點M，連接MD、MN．
求證：
是等腰三角形；
在的條件下，請判斷MD，MN的數量關系和位置關系，并給出證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）如圖，以△ABC的邊AB、AC向外作正方形ABDE和正方形ACFG，試判斷△ABC與△AEG面積之間的關系，并說明理由。
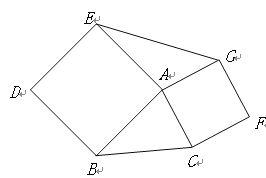
（2）園林小路，曲徑通幽，如圖2所示，小路由白色的正方形理石和黑色的三角形理石鋪成．已知中間的所有正方形的面積之和是a平方米，內圈的所有三角形的面積之和是b平方米，這條小路一共占地多少平方米？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，O為直線AB上一點，∠DOC為直角，OE平分∠AOC，OG平分∠BOC，OF平分∠BOD，下列結論錯誤的是（ ）
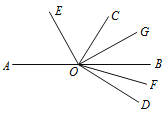
A. ∠DOG與∠BOE互補 B. ∠AOE－∠DOF＝45°
C. ∠EOD與∠COG互補 D. ∠AOE與∠DOF互余
查看答案和解析>>
科目：初中數學 來源： 題型：
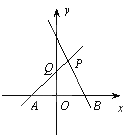
【題目】如圖，直線PA是一次函數y=x+1的圖象，直線PB是一次函數y=-2x+2的圖象.
（1）求A、B、P三點的坐標；
（2）求四邊形PQOB的面積；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在
ABCD中，F是AD的中點，延長BC到點E，使CE=
BC，連結DE，CF。
（1）求證：四邊形CEDF是平行四邊形；
（2）若AB=4，AD=6，∠B=60°，求DE的長。
查看答案和解析>>
科目：初中數學 來源： 題型：
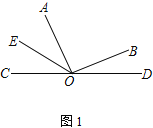
【題目】已知O是直線上的一點，∠AOB是直角，OE平分∠AOC
(1) 在圖①中，若∠BOD＝28°，求∠AOE的度數
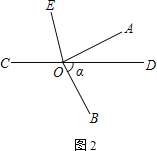
(2) 將圖①中的∠AOB繞頂點O順時針旋轉至圖②的位置．若∠BOD＝α，試用含α的式子表示∠AOE，并說明理由
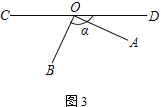
(3) 繼續旋轉AOB至圖③的位置，若∠BOD＝α，其他條件不變，試將圖形補充完整，求∠AOE的度數.（用含α的式子表示）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一次函數y=kx+b（k≠0）與反比例函數y= 
（m≠0）的圖象有公共點A（1，2），D（﹣2，﹣1）．直線l⊥x軸，與x軸交于點N（3，0），與一次函數和反比例函數的圖象分別交于點B，C．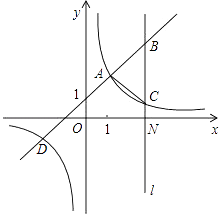 
（1）求一次函數與反比例函數的解析式；
（2）求△ABC的面積；
（3）根據圖象回答，在什么范圍時，一次函數的值大于反比例函數的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某工程隊修建一條長1200米的道路，采用新的施工方式，工效提升了50%，結果提前4天完成任務．
（1）求這個工程隊原計劃每天修建道路多少米？
（2）在這項工程中，如果要求提前2天完成任務，那么實際平均每天修建道路多少米？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com