
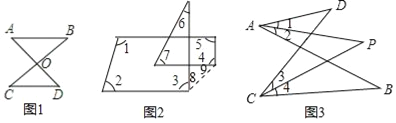
【題目】如圖1我們稱之為“8字形”,請直接寫出∠A,∠B,∠C,∠D之間的數量關系: ;
(2)如圖2,∠1+∠2+∠3+∠4+∠5+∠6+∠7= 度
(3)如圖3所示,已知∠1=∠2,∠3=∠4,猜想∠C,∠P,∠D之間的數量關系,并證明.

【答案】(1)∠A+∠D=∠C+∠B;(2)540°;(3)2∠P=∠D+∠B.
【解析】試題分析: (1)根據三角形內角和定理即可得出∠A+∠D=∠C+∠B;
(2)∠6,∠7的和與∠8,∠9的和相等.由多邊形的內角和得出答案即可;
(3)先根據“8字形”中的角的規律,可得∠DAP+∠D=∠P+∠DCP①,∠PCB+∠B=∠PAB+∠P②,再根據角平分線的定義,得出∠DAP=∠PAB,∠DCP=∠PCB,將①+②,可得2∠P=∠D+∠B,進而求出∠P的度數;
解:(1)如圖1,∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B;
故答案為:∠A+∠D=∠C+∠B;
(2)∵∠6,∠7的和與∠8,∠9的和相等,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠3+∠4+∠5+∠8+∠9=540°.
(3)∠DAP+∠D=∠P+∠DCP,①
∠PCB+∠B=∠PAB+∠P,②
如圖3,∵∠DAB和∠BCD的平分線AP和CP相交于點P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
①+②得:
∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,
即2∠P=∠D+∠B,
又∵∠D=40度,∠B=36度,
∴2∠P=40°+36°,
∴∠P=38°;
故答案為38°.


科目:初中數學 來源: 題型:
【題目】如圖所示,在下列條件中,不能作為判斷△ABD≌△BAC的條件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究應用:用“∪”、“∩”定義兩種新運算:對于兩數a、b,規定a∪b=10a×10b,a∩b=10a÷10b,例如:3∪2=103×102=105,3∩2=103÷102=10.
(1) 求: (2017∪983) 的值
(2) 求: (2018∩2016) 的值;
(3) 當x為何值時, (x∪5)的值與 (23∩17)的值相等.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,直線MN與直線AB、CD分別交于點E、F,∠1與∠2互補.
(1)試判斷直線AB與直線CD的位置關系,并說明理由;
(2)如圖2,∠BEF與∠EFD的角平分線交于點P,EP與CD交于點G,點H是MN上一點,且GH⊥EG,求證:PF∥GH;
(3)如圖3,在(2)的條件下,連接PH,K是GH上一點使∠PHK=∠HPK,作PQ平分∠EPK,問∠HPQ的大小是否發生變化?若不變,請求出其值;若變化,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
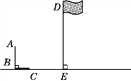
【題目】如圖,九年級(1)班的小明與小艷兩位同學去操場測量旗桿DE的高度,已知直立在地面上的竹竿AB的長為3 m.某一時刻,測得竹竿AB在陽光下的投影BC的長為2 m.
(1)請你在圖中畫出此時旗桿DE在陽光下的投影,并寫出畫圖步驟;
(2)在測量竹竿AB的影長時,同時測得旗桿DE在陽光下的影長為6 m,請你計算旗桿DE的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,M、N分別是AD、BC的中點,P、Q分別是BM、DN的中點.
(1)求證:△MBA≌△NDC;
(2)四邊形MPNQ是什么樣的特殊四邊形?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】仔細閱讀材料,再嘗試解決問題:
完全平方式![]() 以及
以及![]() 的值為非負數的特點在數學學習中有廣泛的應用,比如探求
的值為非負數的特點在數學學習中有廣泛的應用,比如探求![]() 的最大(小)值時,我們可以這樣處理:
的最大(小)值時,我們可以這樣處理:
解:原式 = ![]() .
.
因為無論![]() 取什么數,都有
取什么數,都有![]() 的值為非負數,所以
的值為非負數,所以![]() 的最小值為0;此時
的最小值為0;此時![]() 時,進而
時,進而![]() 的最小值是
的最小值是![]() ;所以當
;所以當![]() 時,原多項式的最小值是
時,原多項式的最小值是![]() .
.
請根據上面的解題思路,探求:
⑴.多項式![]() 的最小值是多少,并寫出對應的
的最小值是多少,并寫出對應的![]() 的取值;
的取值;
⑵.多項式![]() 的最大值是多少,并寫出對應的
的最大值是多少,并寫出對應的![]() 的取值.
的取值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com