
【題目】如圖,G為正方形ABCD的邊AD上的一個動點,AE⊥BG,CF⊥BG,垂足分別為點E,F.已知AD=4,則AE2+CF2= . 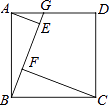
【答案】16
【解析】解:∵四邊形ABCD是正方形,
∴AB=BC=AD=4,∠ABC=90°,
∵AE⊥BG,CF⊥BG,
∴∠AEB=∠CFB=90°,
∵∠ABE+∠CBF=90°,∠CBF+∠BCF=90°,
∴∠ABE=∠BCF,
在△ABE和△BCF中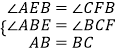 ,
,
∴△AEB≌△BFC,
∴BE=CF,
在Rt△AEB中,∵AE2+BE2=AB2=16,
∴AE2+CF2=16,
所以答案是16.
【考點精析】解答此題的關鍵在于理解正方形的性質的相關知識,掌握正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形.


 應用題作業本系列答案
應用題作業本系列答案科目:初中數學 來源: 題型:
【題目】如圖,是小明從學校到家里行進的路程s(米)與時間t(分)的函數圖象.觀察圖象,從中得到如下信息:①學校離小明家1000米;②小明用了20分鐘到家;③小明前10分鐘走了路程的一半;④小明后10分鐘比前10分鐘走得快,其中正確的有______(填序號).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,AD=2AB,F是AD的中點,作CE⊥AB于E,在線段 AB上,連接EF、CF.則下列結論:①∠BCD=2∠DCF;②∠ECF=∠CEF;③S△BEC=2S△CEF;④∠DFE=3∠AEF,其中一定正確的是( )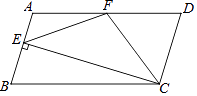
A.②④
B.①②④
C.①②③④
D.②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,方格紙中每個小正方形的邊長都是1個單位長度,△ABC在平面直角坐標系中的位置如圖所示.
(1)將△ABC向上平移3個單位后,得到△A1B1C1,請畫出△A1B1C1,并直接寫出點A1的坐標.
(2)將△ABC繞點O順時針旋轉90°,請畫出旋轉后的△A2B2C2,并求點B所經過的路徑長(結果保留π)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在如圖所示的網格紙中,建立了平面直角坐標系xOy,點P(1,2),點A(2,5),B(﹣2,5),C(﹣2,3).
(1)以點P為對稱中心,畫出△A′B′C′,使△A′B′C′與△ABC關于點P對稱,并寫出下列點的坐標:B′ , C′;
(2)多邊形ABCA′B′C′的面積是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點P1(-4,3)和P2(-4,-3),則P1和P2( )
A. 關于原點對稱 B. 關于y軸對稱
C. 關于x軸對稱 D. 不存在對稱關系
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給出下列命題:
① 對角線相等且互相平分的四邊形是矩形;
② 對角線平分一組對角的平行四邊形是菱形;
③ 對角線互相垂直的矩形是正方形;
④ 對角線相等的菱形是正方形;
其中是真命題的有( )個.
A.1個B.2個C.3個D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com