
【題目】如圖,![]() 中,
中,![]() 點(diǎn)
點(diǎn)![]() 是
是![]() 邊上一點(diǎn),
邊上一點(diǎn),![]() 點(diǎn)
點(diǎn)![]() 是線段
是線段![]() 上的動(dòng)點(diǎn),連接
上的動(dòng)點(diǎn),連接![]() ,以
,以![]() 為斜邊在
為斜邊在![]() 的下方作等腰
的下方作等腰![]() 連接
連接![]() 當(dāng)
當(dāng)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)運(yùn)動(dòng)至點(diǎn)
出發(fā)運(yùn)動(dòng)至點(diǎn)![]() 停止的過(guò)程中,
停止的過(guò)程中,![]() 面積的最大值等于_____________________
面積的最大值等于_____________________![]()
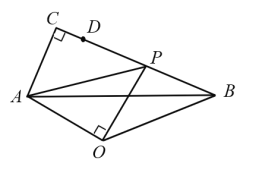
【答案】![]()
【解析】
設(shè)![]() ①當(dāng)
①當(dāng)![]() 時(shí),作
時(shí),作![]() 于
于![]() 于
于![]() .先證明
.先證明![]() ,進(jìn)而可得四邊形
,進(jìn)而可得四邊形![]() 是正方形;設(shè)
是正方形;設(shè)![]() ,用x、y表示出PB和OH,然后運(yùn)用三角形的面積公式二次函數(shù)求最值即可;②當(dāng)
,用x、y表示出PB和OH,然后運(yùn)用三角形的面積公式二次函數(shù)求最值即可;②當(dāng)![]() 時(shí),同理(1)可得
時(shí),同理(1)可得![]() ,根據(jù)二次函數(shù)的性質(zhì)可得,當(dāng)x=4時(shí)有最大值.然后比較即可確定最大值.
,根據(jù)二次函數(shù)的性質(zhì)可得,當(dāng)x=4時(shí)有最大值.然后比較即可確定最大值.
解:設(shè)![]()
①如圖1,當(dāng)![]() 時(shí),作
時(shí),作![]() 于
于![]() 于
于![]() .
.
∴∠OHP=∠OGA=90°
∵四邊形AOPC中,∠C=90°,∠AOP=90°
∴∠CAB+∠OPC=180°
∵∠BPO+∠OPC=180°
∴∠OPH=∠OAG
∵在△AOG和△POH
∠OHP=∠OGA,∠OPH=∠OAG,AO=OP
∴![]() ,
,
∴OH=OG
∵∠OHP=∠OGA=∠C=90°
∴四邊形![]() 是正方形
是正方形
設(shè)![]() ,則
,則![]() ,得
,得![]() ,即有
,即有![]() .
.
∴![]()
∴![]()
所以當(dāng)![]() 時(shí),
時(shí),![]()

②如圖2,當(dāng)![]() 時(shí),同理可得
時(shí),同理可得![]()
所以當(dāng)x=4時(shí),![]()
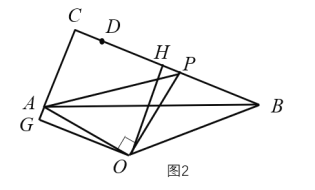
綜上,當(dāng)![]() 時(shí),
時(shí),![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖①,直線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,與
,與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 為線段
為線段![]() 的中點(diǎn),將直線
的中點(diǎn),將直線![]() 向右平移
向右平移![]() 個(gè)單位長(zhǎng)度,
個(gè)單位長(zhǎng)度,![]() 、
、![]() 、
、![]() 的對(duì)應(yīng)點(diǎn)為
的對(duì)應(yīng)點(diǎn)為![]() 、
、![]() 、
、![]() ,反比例函數(shù)
,反比例函數(shù)![]() 的圖象經(jīng)過(guò)點(diǎn)
的圖象經(jīng)過(guò)點(diǎn)![]() ,連接
,連接![]() 、
、![]() .
.
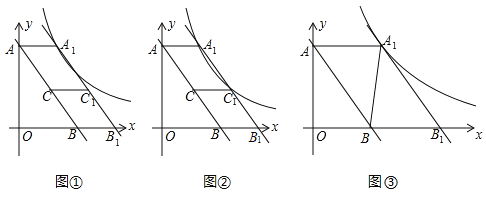
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 的值;
的值;
(2)如圖②, 當(dāng)反比例函數(shù)的圖象經(jīng)過(guò)點(diǎn)![]() 時(shí), 求四邊形
時(shí), 求四邊形![]() 的面積;
的面積;
(3)如圖③,連接![]() ,當(dāng)
,當(dāng)![]() 為等腰三角形時(shí),求
為等腰三角形時(shí),求![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義:如圖1,已知銳角![]() 內(nèi)有定點(diǎn)
內(nèi)有定點(diǎn)![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 任意作一條直線
任意作一條直線![]() ,分別交射線
,分別交射線![]() ,
,![]() 于點(diǎn)M,N.若
于點(diǎn)M,N.若![]() 是線段
是線段![]() 的中點(diǎn)時(shí),則稱(chēng)直線
的中點(diǎn)時(shí),則稱(chēng)直線![]() 是
是![]() 的中點(diǎn)直線.如圖2,射線
的中點(diǎn)直線.如圖2,射線![]() 的解析式為
的解析式為![]() 與
與![]() 軸的夾角為
軸的夾角為![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn)直線.
的中點(diǎn)直線.
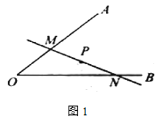
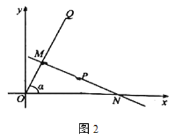
(1)求直線![]() 的解析式;
的解析式;
(2)若過(guò)點(diǎn)![]() 任意作一條直線
任意作一條直線![]() ,分別交射線
,分別交射線![]() ,
,![]() 軸的正半軸于點(diǎn)
軸的正半軸于點(diǎn)![]() ,
,![]() ,記
,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() .求證:
.求證:![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】繪制函數(shù)![]() 的圖象,我們經(jīng)歷了如下過(guò)程:確定自變量
的圖象,我們經(jīng)歷了如下過(guò)程:確定自變量![]() 的取值范圍是
的取值范圍是![]() ;列表-描點(diǎn)--連線,得到該函數(shù)的圖象如圖所示
;列表-描點(diǎn)--連線,得到該函數(shù)的圖象如圖所示
| ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ... |
| ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
| ... |
觀察函數(shù)圖象,回答下列問(wèn)題:
(1)函數(shù)圖象在第 象限;
(2)函數(shù)圖象的對(duì)稱(chēng)性是
B.只是軸對(duì)稱(chēng)圖形,不是中心對(duì)稱(chēng)圖形
A.既是軸對(duì)稱(chēng)圖形,又是中心對(duì)稱(chēng)圖形
D.既不是軸對(duì)稱(chēng)圖形,也不是中心對(duì)稱(chēng)圖形
C.不是軸對(duì)稱(chēng)圖形,而是中心對(duì)稱(chēng)圖形
(3)在![]() 時(shí),當(dāng)
時(shí),當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 有最 (大,小)值,且這個(gè)最值等于
有最 (大,小)值,且這個(gè)最值等于
在![]() 時(shí),當(dāng)
時(shí),當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 有最 (大,小)值,且這個(gè)最值等于
有最 (大,小)值,且這個(gè)最值等于
(4)方程![]() 是否有實(shí)數(shù)解?說(shuō)明
是否有實(shí)數(shù)解?說(shuō)明
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知![]() 是
是![]() 的直徑,點(diǎn)
的直徑,點(diǎn)![]() 是
是![]() 上一點(diǎn),連接
上一點(diǎn),連接![]() ,點(diǎn)
,點(diǎn)![]() 關(guān)于
關(guān)于![]() 的對(duì)稱(chēng)點(diǎn)
的對(duì)稱(chēng)點(diǎn)![]() 恰好落在
恰好落在![]() 上.
上.
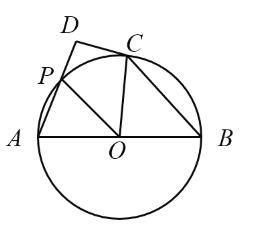
(1)求證:![]() ;
;
(2)過(guò)點(diǎn)![]() 作
作![]() 的切線
的切線![]() ,交
,交![]() 的延長(zhǎng)線于點(diǎn)
的延長(zhǎng)線于點(diǎn)![]() .如果
.如果![]() ,求
,求![]() 的直徑.
的直徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
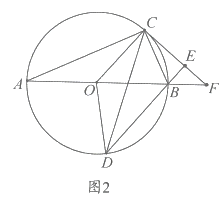
【題目】如圖1,![]() 是
是![]() 的直徑,
的直徑,![]() 為
為![]() 上不同于
上不同于![]() 的兩點(diǎn),連接
的兩點(diǎn),連接![]() 且
且![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() 作
作![]() 垂足為
垂足為![]() 直線
直線![]() 與
與![]() 相交于點(diǎn)
相交于點(diǎn)![]() .
.
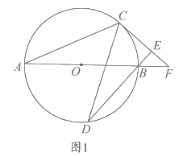
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)若![]()
①求直徑![]() 的長(zhǎng);
的長(zhǎng);
②如圖2所示,連接![]() 直接寫(xiě)出
直接寫(xiě)出![]() 的面積與四邊形
的面積與四邊形![]() 的面積的比值 .
的面積的比值 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某車(chē)行去年A型車(chē)的銷(xiāo)售總額為6萬(wàn)元,今年每輛車(chē)的售價(jià)比去年減少400元.若賣(mài)出的數(shù)量相同,銷(xiāo)售總額將比去年減少20%.
(1)求今年A型車(chē)每輛車(chē)的售價(jià).
(2)該車(chē)行計(jì)劃新進(jìn)一批A型車(chē)和B型車(chē)共45輛,已知A、B型車(chē)的進(jìn)貨價(jià)格分別是1100元,1400元,今年B型車(chē)的銷(xiāo)售價(jià)格是2000元,要求B型車(chē)的進(jìn)貨數(shù)量不超過(guò)A型車(chē)數(shù)量的兩倍,應(yīng)如何進(jìn)貨才能使這批車(chē)獲得最大利潤(rùn),最大利潤(rùn)是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】北京和上海都有檢測(cè)新冠肺炎病毒的儀器可供外地使用,其中北京有![]() 臺(tái),上海有
臺(tái),上海有![]() 臺(tái).
臺(tái).
(1)已知武漢需要![]() 臺(tái),溫州需要
臺(tái),溫州需要![]() 臺(tái),從北京、上海將儀器運(yùn)往武漢、溫州的費(fèi)用如下表所示,有關(guān)部門(mén)計(jì)劃用
臺(tái),從北京、上海將儀器運(yùn)往武漢、溫州的費(fèi)用如下表所示,有關(guān)部門(mén)計(jì)劃用![]() 元運(yùn)送這些儀器.請(qǐng)你設(shè)計(jì)一種運(yùn)送方案,使武漢、溫州能得到所需儀器,而且運(yùn)費(fèi)正好夠用.
元運(yùn)送這些儀器.請(qǐng)你設(shè)計(jì)一種運(yùn)送方案,使武漢、溫州能得到所需儀器,而且運(yùn)費(fèi)正好夠用.
(2)為了節(jié)約運(yùn)送資金,中央防控工作組統(tǒng)一調(diào)配儀器,分配到溫州的儀器不能超過(guò)![]() 臺(tái),則如何調(diào)配?
臺(tái),則如何調(diào)配?
終點(diǎn) 起點(diǎn) | 溫州 | 武漢 |
北京 |
|
|
上海 |
|
|
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
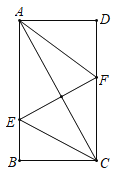
【題目】如圖,在矩形ABCD中,AD=2,AB=4,E、F分別是AB、CD邊上的動(dòng)點(diǎn),EF⊥AC,則AF+CE的最小值為________.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com