
【題目】如圖,已知△ABC中,AB=AC,把△ABC繞A點沿順時針方向旋轉得到△ADE,連接BD,CE交于點F.
(1)求證:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,當四邊形ADFC是菱形時,求BF的長.

【答案】(1)證明見解析(2)2![]() -2
-2
【解析】試題分析:
(1)由旋轉的性質易得:AD=AB,AE=AC,∠DAE=∠BAC,結合已知和圖形可得AD=AC=AB=AE,∠EAC=∠DAB,再由“SAS”可證△AEC≌△ADB;
(2)由四邊形ADFC是菱形可得DF=AC=AB=2,AC∥DF,從而可得∠DBA=∠BAC=45°,再由AD=AB可得∠BDA=∠DBA=45°,就能證明△ADB是等腰直角三角形,由勾股定理可得BD的長,最后由BD-DF可得BF的長.
試題解析:
(1)由旋轉的性質得△ABC≌△ADE,且AB=AC,
∴AE=AD=AC=AB,∠BAC=∠DAE,
∴∠BAC+∠BAE=∠DAE+∠BAE,即∠CAE=∠BAD.
∵在△AEC和△ADB中, 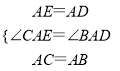 ,
,
∴△AEC≌△ADB(SAS);
(2)∵四邊形ADFC是菱形,
∴DF=AC=AB=2,AC∥DF.
∴∠DBA=∠BAC=45°.
由(1)可知AB=AD,
∴∠DBA=∠BDA=45°,
∴△ABD為直角邊長為2的等腰直角三角形,
∴BD2=AB2+AD2,即BD2=8,解得BD=![]() ,
,
∴BF=BD-DF=![]() -2.
-2.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:初中數學 來源: 題型:
【題目】如圖,甲、乙兩個圓柱形玻璃容器各盛有一定量的液體, 甲、乙容器的內底面半徑分別為![]() 和
和![]() ,現將一個半徑為
,現將一個半徑為![]() 的圓柱形玻璃棒(足夠長)垂直觸底插入甲容器,此時甲、乙兩個容器的液面高均為
的圓柱形玻璃棒(足夠長)垂直觸底插入甲容器,此時甲、乙兩個容器的液面高均為![]() (如圖甲),再將此玻璃棒垂直觸底插入乙容器(液體損耗忽略不計),此時乙容器的液面比甲容器的液面高
(如圖甲),再將此玻璃棒垂直觸底插入乙容器(液體損耗忽略不計),此時乙容器的液面比甲容器的液面高![]() (如圖乙).
(如圖乙).
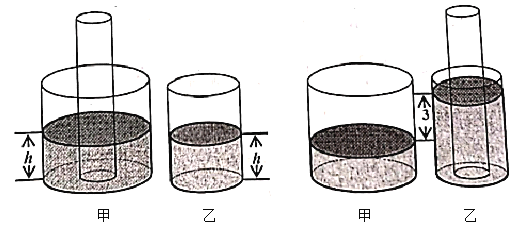
(1)求甲、乙兩個容器的內底面面積.
(2)求甲容器內液體的體積(用含![]() 的代數式表示).
的代數式表示).
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】元旦放假時,小明一家三口一起乘小轎車去探望爺爺、奶奶和姥爺、姥姥.早上從家里出發,向東走了5千米到超市買東西,然后又向東走了2.5千米到爺爺家,下午從爺爺家出發向西走了10千米到姥爺家,晚上返回家里.
(1)若以小明家為原點,向東為正方向,用1個單位長度表示1千米,請將超市、爺爺家和姥爺家的位置在下面數軸上分別用點A、B、C表示出來;
![]()
(2)超市和姥爺家相距多少千米?
(3)若小轎車每千米耗油0.08升,求小明一家從出發到返回家,小轎車的耗油量.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知數軸上點A表示的數為a,點B表示的數為b,且滿足![]() .
.
(1)寫出a、b及AB的距離:a=________;b=________;AB=________.
(2)若動點P從點A出發,以每秒3個點位長度沿數軸向右勻速運動,動點Q從點B出發,以每秒5個單位長度向右勻速運動,若P、Q同時出發,問點Q運動多少秒追上點P?
![]()
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】湘潭市繼2017年成功創建全國文明城市之后,又準備爭創全國衛生城市.某小區積極響應,決定在小區內安裝垃圾分類的溫馨提示牌和垃圾箱,若購買2個溫馨提示牌和3個垃圾箱共需550元,且垃圾箱的單價是溫馨提示牌單價的3倍.
(1)求溫馨提示牌和垃圾箱的單價各是多少元?
(2)該小區至少需要安放48個垃圾箱,如果購買溫馨提示牌和垃圾箱共100個,且費用不超過10000元,請你列舉出所有購買方案,并指出哪種方案所需資金最少?最少是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示是一個正方體的表面展開圖,請回答下列問題:
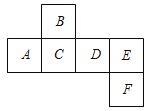
(1)與面B、面C相對的面分別是 和 ;
(2)若A=a3+![]() a2b+3,B=﹣
a2b+3,B=﹣![]() a2b+a3,C=a3﹣1,D=﹣
a2b+a3,C=a3﹣1,D=﹣![]() (a2b+15),且相對兩個面所表示的代數式的和都相等,求E、F代表的代數式.
(a2b+15),且相對兩個面所表示的代數式的和都相等,求E、F代表的代數式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,M,N,P,R分別是數軸上的四個整數所對應的點,其中有一個點是原點,并且,MN=NP=PR=1,數a對應的點在M和N之間,數b對應的點在P和R之間,若|a|+|b|=2,則原點是(填M,N,P,R中的一個或幾個)_____________

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我鄉某校舉行全體學生“定點投籃”比賽,每位學生投40個,隨機抽取了部分學生的投籃結果,并繪制成如下統計圖表。
組別 | 投進個數 | 人數 |
A |
| 10 |
B |
| 15 |
C |
| 30 |
D |
| m |
E |
| n |
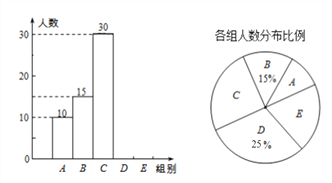
根據以上信息完成下列問題。
①本次抽取的學生人數為多少?
②統計表中的m=__________;
③扇形統計圖中E組所占的百分比;
④補全頻數分布直方圖;
⑤扇形統計圖中“C組”所對應的圓心角的度數;
⑥本次比賽中投籃個數的中位數落在哪一組;
⑦已知該校共有900名學生,如投進個數少于24個定為不合格,請你估計該校本次投籃比賽不合格的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1所示矩形ABCD中,BC=x,CD=y,y與x滿足的反比例函數關系如圖2所示,等腰直角三角形AEF的斜邊EF過C點,M為EF的中點,則下列結論正確的是

A. 當x=3時,EC<EM B. 當y=9時,EC>EM
C. 當x增大時,EC·CF的值增大。 D. 當y增大時,BE·DF的值不變。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com