
【題目】如圖,在平面直角坐標(biāo)系中,反比例函數(shù)![]() 的圖像與邊長是6的正方形
的圖像與邊長是6的正方形![]() 的兩邊
的兩邊![]() ,
,![]() 分別相交于
分別相交于![]() ,
,![]() 兩點.
兩點.
(1)若點![]() 是
是![]() 邊的中點,求反比例函數(shù)
邊的中點,求反比例函數(shù)![]() 的解析式和點
的解析式和點![]() 的坐標(biāo);
的坐標(biāo);
(2)若![]() ,求直線
,求直線![]() 的解析式及
的解析式及![]() 的面積
的面積

【答案】(1)![]() ,N(3,6);(2)y=-x+8,S△OMN=16.
,N(3,6);(2)y=-x+8,S△OMN=16.
【解析】
(1)求出點M坐標(biāo),利用待定系數(shù)法即可求得反比例函數(shù)的解析式,把N點的縱坐標(biāo)代入解析式即可求得橫坐標(biāo);
(2)根據(jù)M點的坐標(biāo)與反比例函數(shù)的解析式,求得N點的坐標(biāo),利用待定系數(shù)法求得直線MN的解析式,根據(jù)△OMN=S正方形OABC-S△OAM-S△OCN-S△BMN即可得到答案.
解:(1)∵點M是AB邊的中點,∴M(6,3).
∵反比例函數(shù)y=![]() 經(jīng)過點M,∴3=
經(jīng)過點M,∴3=![]() .∴k=18.
.∴k=18.
∴反比例函數(shù)的解析式為y=![]() .
.
當(dāng)y=6時,x=3,∴N(3,6).
(2)由題意,知M(6,2),N(2,6).
設(shè)直線MN的解析式為y=ax+b,則
![]() ,
,
解得![]() ,
,
∴直線MN的解析式為y=-x+8.
∴S△OMN=S正方形OABC-S△OAM-S△OCN-S△BMN=36-6-6-8=16.


 尖子生新課堂課時作業(yè)系列答案
尖子生新課堂課時作業(yè)系列答案 英才計劃同步課時高效訓(xùn)練系列答案
英才計劃同步課時高效訓(xùn)練系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 分別是斜邊
分別是斜邊![]() 上的高,中線,
上的高,中線,![]() ,
,![]() .
.
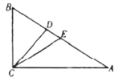
(1)若![]() ,
,![]() ,求
,求![]() 的長;
的長;
(2)直接寫出:![]() _______(用含
_______(用含![]() ,
,![]() 的代數(shù)式表示);
的代數(shù)式表示);
(3)若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,動點
,動點![]() 在射線
在射線![]() 上,以
上,以![]() 為半徑的
為半徑的![]() 交邊
交邊![]() 于點
于點![]() (點
(點![]() 與點
與點![]() 不重合),聯(lián)結(jié)
不重合),聯(lián)結(jié)![]() 、
、![]() ,設(shè)
,設(shè)![]() ,
,![]() .
.
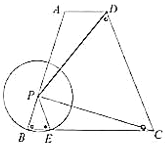
(1)求證:![]() ;
;
(2)求![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式,并寫出定義域;
的函數(shù)解析式,并寫出定義域;
(3)聯(lián)結(jié)![]() ,當(dāng)
,當(dāng)![]() 時,以
時,以![]() 為圓心半徑為
為圓心半徑為![]() 的
的![]() 與
與![]() 相交,求
相交,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,雙曲線![]() 經(jīng)過矩形OABC的邊BC的中點E,交AB于點D.設(shè)點B的坐標(biāo)為(m,n).
經(jīng)過矩形OABC的邊BC的中點E,交AB于點D.設(shè)點B的坐標(biāo)為(m,n).
(1)直接寫出點E的坐標(biāo),并求出點D的坐標(biāo);(用含m,n的代數(shù)式表示)
(2)若梯形ODBC的面積為![]() ,求雙曲線的函數(shù)解析式.
,求雙曲線的函數(shù)解析式.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖是由7個同樣大小的正方體擺成的幾何體.將正方體①移走后,所得幾何體( )
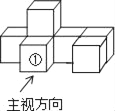
A. 主視圖改變,俯視圖改變 B. 左視圖改變,俯視圖改變
C. 俯視圖不變,左視圖改變 D. 主視圖不變,左視圖不變
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
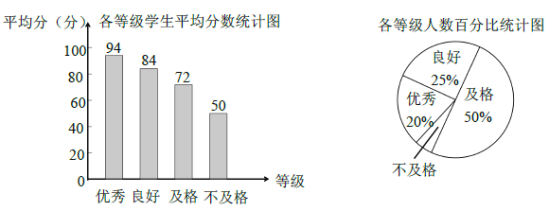
【題目】《中學(xué)生體質(zhì)健康標(biāo)準(zhǔn)》規(guī)定學(xué)生體質(zhì)健康等級標(biāo)準(zhǔn)為:90分及以上為優(yōu)秀;80分~89分為良好;60分~79分為及格;59分及以下為不及格. 某校從九年級學(xué)生中隨機抽取了![]() 的學(xué)生進(jìn)行了體質(zhì)測試,得分情況如下圖.
的學(xué)生進(jìn)行了體質(zhì)測試,得分情況如下圖.
(1)在抽取的學(xué)生中不及格人數(shù)所占的百分比是 ,它的圓心角度數(shù)為 度.
(2)小明按以下方法計算出抽取的學(xué)生平均得分是:![]() . 根據(jù)所學(xué)的統(tǒng)計知識判斷小明的計算是否正確,若不正確,請計算正確結(jié)果.
. 根據(jù)所學(xué)的統(tǒng)計知識判斷小明的計算是否正確,若不正確,請計算正確結(jié)果.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校九年級數(shù)學(xué)小組在課外活動中,研究了同一坐標(biāo)系中兩個反比例函數(shù)![]() 與
與![]()
![]() 在第一象限圖象的性質(zhì),經(jīng)歷了如下探究過程:
在第一象限圖象的性質(zhì),經(jīng)歷了如下探究過程:
操作猜想:
(1)如圖①,當(dāng)![]() ,
,![]() 時,在
時,在![]() 軸的正方向上取一點
軸的正方向上取一點![]() 作
作![]() 軸的平行線交
軸的平行線交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .當(dāng)
.當(dāng)![]() 時,
時,![]() ________,
________,![]() ________,
________,![]() ________;當(dāng)
________;當(dāng)![]() 時,
時,![]() ________,
________,![]() ________,
________,![]() ________;當(dāng)
________;當(dāng)![]() 時,猜想
時,猜想![]() ________.
________.

數(shù)學(xué)思考:
(2)在![]() 軸的正方向上任意取點
軸的正方向上任意取點![]() 作
作![]() 軸的平行線,交
軸的平行線,交![]() 于點
于點![]() 、交
、交![]() 于點
于點![]() ,請用含
,請用含![]() 、
、![]() 的式子表示
的式子表示![]() 的值,并利用圖②加以證明.
的值,并利用圖②加以證明.

推廣應(yīng)用:
(3)如圖③,若![]() ,
,![]() ,在
,在![]() 軸的正方向上分別取點
軸的正方向上分別取點![]() 、
、![]()
![]() 作
作![]() 軸的平行線,交
軸的平行線,交![]() 于點
于點![]() 、
、![]() ,交
,交![]() 于點
于點![]() 、
、![]() ,是否存在四邊形
,是否存在四邊形![]() 是正方形?如果存在,求
是正方形?如果存在,求![]() 的長和點
的長和點![]() 的坐標(biāo);如果不存在,請說明理由.
的坐標(biāo);如果不存在,請說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方形ABCD中,對角線AC與BD交于點O,在Rt△PFE中,∠EPF=90°,點E、F分別在邊AD、AB上.
(1)如圖1,若點P與點O重合:①求證:AF=DE;②若正方形的邊長為2![]() ,當(dāng)∠DOE=15°時,求線段EF的長;
,當(dāng)∠DOE=15°時,求線段EF的長;
(2)如圖2,若Rt△PFE的頂點P在線段OB上移動(不與點O、B重合),當(dāng)BD=3BP時,證明:PE=2PF.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com