
【題目】(1)如圖1,已知⊙O的半徑是4,△ABC內接于⊙O,AC=![]() .
.
①求∠ABC的度數;
②已知AP是⊙O的切線,且AP=4,連接PC.判斷直線PC與⊙O的位置關系,并說明理由;
(2)如圖2,已知ABCD的頂點A、B、D在⊙O上,頂點C在⊙O內,延長BC交⊙O于點E,連接DE.求證:DE=DC.

【答案】(1)45°;②直線PC與⊙O相切.理由見解析;(2)證明見解析.
【解析】試題分析:(1)①連結OA、OC,如圖1,利用勾股定理的逆定理證明△OCA為等腰直角三角形,∠AOC=90°,然后根據圓周角定理易得∠ABC=45°;
②先根據切線的性質得∠OAP=90°,再證四邊形APCO為平行四邊形,加上∠AOC=90°,則可判斷四邊形AOCP為矩形,所以∠PCO=90°,然后根據切線得判斷定理得到PC為⊙O的切線;
(2)根據平行四邊形的性質得AB∥CD,AD∥BC,再由平行線的性質得∠B+∠A=180°,∠DCE=∠B,由圓內接四邊形的性質得∠E+∠A=180°,易得∠DCE=∠E,則根據等腰三角形的判定定理即可得到DC=DE.
試題解析:(1)解:①連結OA、OC,如圖1,
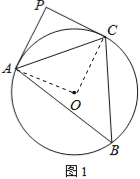
∵OA=OC=4,AC=4![]() ,
,
∴OA2+OC2=AC2,
∴△OCA為等腰直角三角形,∠AOC=90°,
∴∠ABC=![]() ∠AOC=45°;
∠AOC=45°;
②直線PC與⊙O相切.理由如下:
∵AP是⊙O的切線,
∴∠OAP=90°,
而∠AOC=90°,
∴AP∥OC,
而AP=OC=4,
∴四邊形APCO為平行四邊形,
∵∠AOC=90°,
∴四邊形AOCP為矩形,
∴∠PCO=90°,
∴PC⊥OC,
∴PC為⊙O的切線;
(2)證明:∵四邊形ABCD為平行四邊形,
∴AB∥CD,AD∥BC,
∴∠B+∠A=180°,∠DCE=∠B,
∵∠E+∠A=180°,
∴∠E=∠B,
∴∠DCE=∠E,
∴DC=DE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,點C、D、E三點在同一直線上,連接BD. 
求證:
(1)△BAD≌△CAE;
(2)試猜想BD、CE有何特殊位置關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
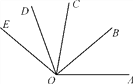
【題目】如圖,OB為∠AOC的平分線,OD是∠COE的平分線.
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD為多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB為多少度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC為等邊三角形,D、E分別為BC、AC邊上的兩動點(與點A、B、C不重合),且總使CD=AE,AD與BE相交于點F. 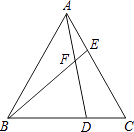
(1)求證:AD=BE;
(2)求∠BFD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,數軸上A,B兩點對應的有理數分別為10和15,點P從點A出發,以每秒1個單位長度的速度沿數軸正方向運動,點Q同時從原點O出發,以每秒2個單位長度的速度沿數軸正方向運動,設運動時間為t秒.
![]()
(1)當0<t<5時,用含t的式子填空:
BP=_______,AQ=_______;
(2)當t=2時,求PQ的值;
(3)當PQ=![]() AB時,求t的值.
AB時,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列事件中最適合使用普查方式收集數據的是( )
A.為制作校服,了解某班同學的身高情況
B.了解全市初三學生的視力情況
C.了解一種節能燈的使用壽命
D.了解我省農民的年人均收入情況
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com