
【題目】如圖,帆船A和帆船B在太湖湖面上訓(xùn)練,O為湖面上的一個定點,教練船靜候于O點,訓(xùn)練時要求A、B兩船始終關(guān)于O點對稱.以O為原點,建立如圖所示的坐標(biāo)系,x軸、y軸的正方向分別表示正東、正北方向.設(shè)A、B兩船可近似看成在雙曲線y=![]() 上運動,湖面風(fēng)平浪靜,雙帆遠(yuǎn)影優(yōu)美,訓(xùn)練中當(dāng)教練船與A、B兩船恰好在直線y=x上時,三船同時發(fā)現(xiàn)湖面上有一遇險的C船,此時教練船測得C船在東南45°方向上,A船測得AC與AB的夾角為60°,B船也同時測得C船的位置(假設(shè)C船位置不再改變,A、B、C三船可分別用A、B、C三點表示).
上運動,湖面風(fēng)平浪靜,雙帆遠(yuǎn)影優(yōu)美,訓(xùn)練中當(dāng)教練船與A、B兩船恰好在直線y=x上時,三船同時發(fā)現(xiàn)湖面上有一遇險的C船,此時教練船測得C船在東南45°方向上,A船測得AC與AB的夾角為60°,B船也同時測得C船的位置(假設(shè)C船位置不再改變,A、B、C三船可分別用A、B、C三點表示).
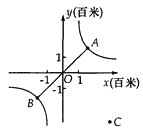
(1)發(fā)現(xiàn)C船時,A、B、C三船所在位置的坐標(biāo)分別為A(_______,_______)、B(_______,_______)和C(_______,_______);
(2)發(fā)現(xiàn)C船,三船立即停止訓(xùn)練,并分別從A、O、B三點出發(fā)沿最短路線同時前往救援,設(shè)A、B兩船的速度相等,教練船與A船的速度之比為3:4,問教練船是否最先趕到?請說明理由.
【答案】(1)A(2,2),B(-2,-2),C(2![]() ,-2
,-2![]() );(2)教練船沒有最先趕到,理由見詳解.
);(2)教練船沒有最先趕到,理由見詳解.
【解析】
(1)A、B兩點直線y=x上和雙曲線y=![]() ,列方程組可求A、B兩點坐標(biāo),在依題意判斷△ABC為等邊三角形,OA=2
,列方程組可求A、B兩點坐標(biāo),在依題意判斷△ABC為等邊三角形,OA=2![]() ,則OC=
,則OC=![]() OA=2
OA=2![]() ,過C點作x軸的垂線CE,垂足為E,利用OC在第四象限的角平分線上求OE,CE,確定C點坐標(biāo);
,過C點作x軸的垂線CE,垂足為E,利用OC在第四象限的角平分線上求OE,CE,確定C點坐標(biāo);
(2)分別求出AC、OC的長,分別表示教練船與A、B兩船的速度與時間,比較時間的大小即可.
解:(1)CE⊥x軸于E,解方程組![]()
得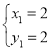 ,
,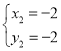
∴A(2,2),B(-2,-2),
在等邊△ABC中可求OA=2![]() ,
,
則OC=![]() OA=2
OA=2![]() ,
,
在Rt△OCE中,![]() ,
,
∴C(2![]() ,-2
,-2![]() );
);
(2)作AD⊥x軸于D,連AC、BC和OC,

∵A(2,2),
∴∠AOD=45°,AO=2![]() ,
,
∵C在O的東南45°方向上,
∴∠AOC=45°+45°=90°,
∵AO=BO,∴AC=BC,
又∵∠BAC=60°,
∴△ABC為正三角形,
∴AC=BC=AB=2AO=4![]() ,
,
∴![]() ,
,
由條件設(shè)教練船的速度為3m,A、B兩船的速度都為4m,
則教練船所用時間為![]() ,A、B兩船所用時間均為
,A、B兩船所用時間均為![]() =
=![]() ,
,
∵![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() >
>![]() ;
;
∴教練船沒有最先趕到.


科目:初中數(shù)學(xué) 來源: 題型:
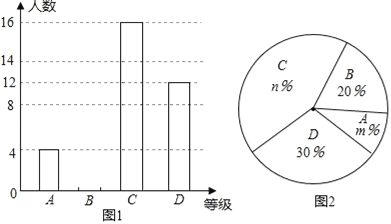
【題目】2016年3月,我市某中學(xué)舉行了“愛我中國朗誦比賽”活動,根據(jù)學(xué)生的成績劃分為A、B、C、D四個等級,并繪制了不完整的兩種統(tǒng)計圖.根據(jù)圖中提供的信息,回答下列問題:
(1)參加朗誦比賽的學(xué)生共有 人,并把條形統(tǒng)計圖補充完整;
(2)扇形統(tǒng)計圖中,m= ,n= ;C等級對應(yīng)扇形有圓心角為 度;
(3)學(xué)校欲從獲A等級的學(xué)生中隨機(jī)選取2人,參加市舉辦的朗誦比賽,請利用列表法或樹形圖法,求獲A等級的小明參加市朗誦比賽的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】類比、轉(zhuǎn)化、從特殊到一般等思想方法,在數(shù)學(xué)學(xué)習(xí)和研究中經(jīng)常用到,如下是一個案例,請補充完整.
原題:如圖1,在平行四邊形![]() 中,點
中,點![]() 是
是![]() 邊上的中點,點
邊上的中點,點![]() 是線段
是線段![]() 上一點,
上一點,![]() 的延長線交射線
的延長線交射線![]() 于點
于點![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
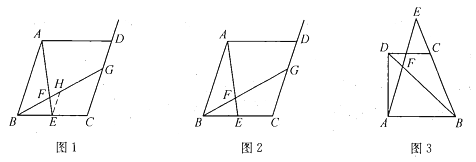
(1)嘗試探究
在圖1中,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,則
,則![]() 和
和![]() 的數(shù)量關(guān)系是______,
的數(shù)量關(guān)系是______,![]() 和
和![]() 的數(shù)量關(guān)系是______,
的數(shù)量關(guān)系是______,![]() 的值是______;
的值是______;
(2)類比延伸
如圖2,在原題的條件下,當(dāng)![]() 時,參照問題(1)的研究結(jié)論,請你猜想
時,參照問題(1)的研究結(jié)論,請你猜想![]() 的值(用含
的值(用含![]() 的代數(shù)式表示),并證明你的猜想;
的代數(shù)式表示),并證明你的猜想;
(3)拓展遷移
如圖3,梯形![]() 中,
中,![]() ,點
,點![]() 是
是![]() 延長線上一點,
延長線上一點,![]() 和
和![]() 相交于點
相交于點![]() ,當(dāng)
,當(dāng)![]() ,
,![]() 時,請你求出
時,請你求出![]() 的值(用含
的值(用含![]() 、
、![]() 的代數(shù)式表示).
的代數(shù)式表示).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
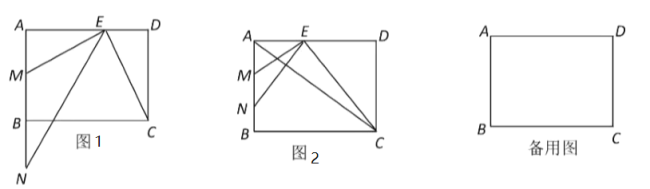
【題目】在矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是邊
是邊![]() 上一點,
上一點,![]() 交
交![]() 于點
于點![]() ,點
,點![]() 在射線
在射線![]() 上,且
上,且![]() 是
是![]() 和
和![]() 的比例中項.
的比例中項.
(1)如圖1,求證:![]() ;
;
(2)如圖2,當(dāng)點![]() 在線段
在線段![]() 之間,聯(lián)結(jié)
之間,聯(lián)結(jié)![]() ,且
,且![]() 與
與![]() 互相垂直,求
互相垂直,求![]() 的長;
的長;
(3)聯(lián)結(jié)![]() ,如果
,如果![]() 與以點
與以點![]() 、
、![]() 、
、![]() 為頂點所組成的三角形相似,求
為頂點所組成的三角形相似,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知拋物線經(jīng)過![]() ,
,![]() 及原點
及原點![]() ,頂點為
,頂點為![]() .
.
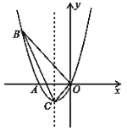
(1)求拋物線的函數(shù)解析式;
(2)設(shè)點![]() 在拋物線上,點
在拋物線上,點![]() 在拋物線的對稱軸上,且以
在拋物線的對稱軸上,且以![]() 、
、![]() 、
、![]() ,
,![]() 為頂點,
為頂點,![]() 為邊的四邊形是平行四邊形,求點
為邊的四邊形是平行四邊形,求點![]() 的坐標(biāo);
的坐標(biāo);
(3)![]() 是拋物線上第一象限內(nèi)的動點,過點
是拋物線上第一象限內(nèi)的動點,過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() .是否存在這樣的點
.是否存在這樣的點![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?若存在,求出點
相似?若存在,求出點![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,等腰△ABC 紙板中, AB =AC=5 , BC = 2 ,P為AB上一點,過P沿直線剪下一個與△ABC 相似的小三角形紙板,恰有 3 種不同的剪法,那么BP長可以為( ).

A.3.6B.2.6C.1.6D.0.6
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線y=ax2+bx+c(a≠0)上部分點的橫坐標(biāo)x與縱坐標(biāo)y的對應(yīng)值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求該拋物線的表達(dá)式;
(2)已知點E(4, y)是該拋物線上的點,點E關(guān)于拋物線的對稱軸對稱的點為點F,求點E和點F的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直角坐標(biāo)平面xOy中,點A坐標(biāo)為![]() ,
,![]() ,
,![]() ,AB與x軸交于點C,那么AC:BC的值為______.
,AB與x軸交于點C,那么AC:BC的值為______.
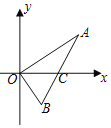
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
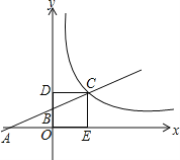
【題目】如圖,直線y1=kx+1分別交x軸,y軸于點A.B,交反比例函數(shù)y2=![]() (x>0)的圖象于點C,CD⊥y軸于點D,CE⊥x軸于點E,S△OAB=1,
(x>0)的圖象于點C,CD⊥y軸于點D,CE⊥x軸于點E,S△OAB=1,![]() =
=![]() .
.
(1)點A的坐標(biāo)為______;
(2)求直線和反比例函數(shù)的解析式;
(3)根據(jù)圖象直接回答:在第一象限內(nèi),當(dāng)x取何值時,y1≥y2.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com