
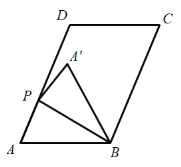
【題目】如圖,在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射線
是射線![]() 上一點,連接
上一點,連接![]() ,沿
,沿![]() 將三角形
將三角形![]() 折疊,得三角形
折疊,得三角形![]() .
.
(1)當![]() 時,
時,![]() =_______度;
=_______度;
(2)如圖,當![]() 時,求線段
時,求線段![]() 的長度;
的長度;

(3)當點![]() 落在平行四邊形
落在平行四邊形![]() 的邊上時,直接寫出線段
的邊上時,直接寫出線段![]() 的長度.
的長度.
【答案】(1)85或95或5;(2)![]() ;(3)
;(3)![]() 或9
或9
【解析】
(1)根據點P在線段AD上或AD的延長線上和點![]() 與AD的位置關系分類討論,分別畫出圖形,根據折疊的性質即可求出結論;
與AD的位置關系分類討論,分別畫出圖形,根據折疊的性質即可求出結論;
(2)根據平行四邊形的性質可推出![]() ,從而得出
,從而得出![]() ,作
,作![]() 于
于![]() ,根據銳角三角函數和勾股定理求出AH和BH,利用銳角三角函數求出PH,即可求出結論;
,根據銳角三角函數和勾股定理求出AH和BH,利用銳角三角函數求出PH,即可求出結論;
(3)分點![]() 落在AD、BC、CD和AB上討論,分別畫出對應的圖形,根據折疊的性質、銳角三角函數和勾股定理即可分別求出結論.
落在AD、BC、CD和AB上討論,分別畫出對應的圖形,根據折疊的性質、銳角三角函數和勾股定理即可分別求出結論.
解:(1)①當點P在線段AD上,且點![]() 在直線AD右側時,如下圖所示
在直線AD右側時,如下圖所示
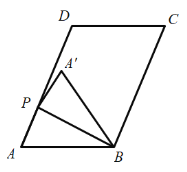
由折疊的性質可得![]() ;
;
②當點P在線段AD上,且點![]() 在直線AD左側時,如下圖所示
在直線AD左側時,如下圖所示
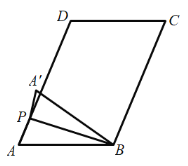
由折疊的性質可得![]() ;
;
③當點P在線段AD的延長線上時,如下圖所示
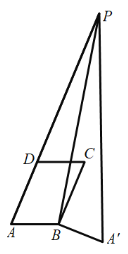
由折疊的性質可得![]()
綜上:![]() =85°或95°或5°
=85°或95°或5°
故答案為:85或95或5;
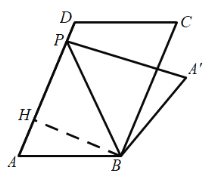
(2)在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
作![]() 于
于![]() ,如下圖,
,如下圖,
∴![]() ,
,
∴設![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)①當點![]() 在
在![]() 上時,如下圖,
上時,如下圖,
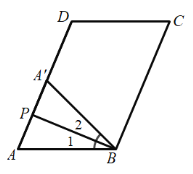
∵![]() ,
,
∴![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
設![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②當![]() 在
在![]() 上時,如下圖
上時,如下圖

由折疊可知,![]() ,
,![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴四邊形![]() 為菱形,
為菱形,
∴![]() ;
;
③當![]() 在CD上時,如下圖,過點D作DM⊥AB于M,過點B作BN⊥CD于N
在CD上時,如下圖,過點D作DM⊥AB于M,過點B作BN⊥CD于N
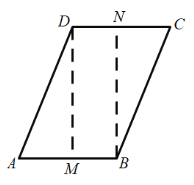
∴DM=BN,
∵![]()
設![]() ,
,![]() ,
,
∴![]() ,
,
解得:x=1
∴BN=DM=12
∵![]() 在CD上
在CD上
∴![]() ≥BN=12>BA
≥BN=12>BA
∴此種情況不存在;
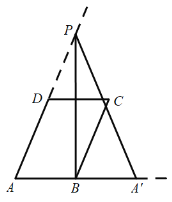
④當![]() 在AB上時,如下圖,根據折疊的性質可得點
在AB上時,如下圖,根據折疊的性質可得點![]() 與點A關于PB對稱,即點
與點A關于PB對稱,即點![]() 在AB的延長線上,不符合題意.
在AB的延長線上,不符合題意.
綜上:當點![]() 落在平行四邊形
落在平行四邊形![]() 的邊上時,
的邊上時,![]() 或9;
或9;


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標中,拋物線y=ax2+bx+c過點A(﹣1,0),B(3,0),C(0,3),點P是直線BC上方拋物線上的一動點,PE∥y軸,交直線BC于點E連接AP,交直線BC于點 D.
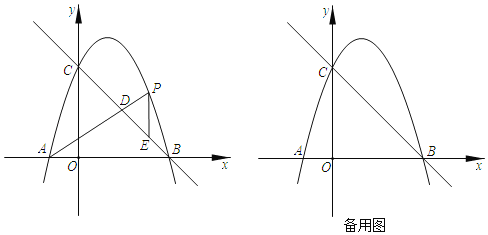
(1)求拋物線的函數表達式;
(2)當AD=2PD時,求點P的坐標;
(3)求線段![]() 的最大值;
的最大值;
(4)當線段![]() 最大時,若點F在直線BC上且∠EFP=2∠ACO,直接寫出點F的坐標.
最大時,若點F在直線BC上且∠EFP=2∠ACO,直接寫出點F的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知⊙O的半徑長為1,AB、AC是⊙O的兩條弦,且AB=AC,BO的延長線交AC于點D,連接OA、OC.
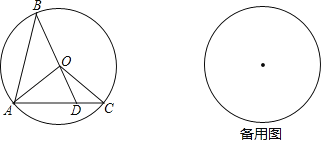
(1)求證:△OAD∽△ABD;
(2)當△OCD是直角三角形時,求B、C兩點的距離;
(3)記△AOB、△AOD、△COD的面積分別為S1、S2、S3,如果S22=S1S3,試證明點D為線段AC的黃金分割點.
查看答案和解析>>
科目:初中數學 來源: 題型:
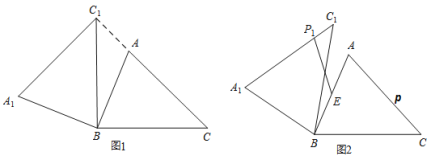
【題目】在銳角![]() 中,
中,![]() ,
,![]() ,
,![]() ,將
,將![]() 繞點
繞點![]() 按逆時針方向旋轉,得到
按逆時針方向旋轉,得到![]() .(1)如圖1,當點
.(1)如圖1,當點![]() 在線段
在線段![]() 的延長線上時,則
的延長線上時,則![]() 的度數為______________度;(2)如圖2,點
的度數為______________度;(2)如圖2,點![]() 為線段
為線段![]() 中點,點
中點,點![]() 是線段
是線段![]() 上的動點,在
上的動點,在![]() 繞點
繞點![]() 按逆時針方向旋轉過程中,點
按逆時針方向旋轉過程中,點![]() 的對應點是點
的對應點是點![]() ,則線段
,則線段![]() 長度最小值是_____________.
長度最小值是_____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,對角線AC、BD相交于點O,過點D作對角線BD的垂線交BA的延長線于點E.

(1)證明:四邊形ACDE是平行四邊形;
(2)若AC=8,BD=6,求△ADE的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,點
,點![]() 在邊
在邊![]() 上運動(不與點
上運動(不與點![]() ,
,![]() 重合),以
重合),以![]() 為邊作正方形
為邊作正方形![]() ,使點
,使點![]() 在正方形
在正方形![]() 內,連接
內,連接![]() ,則下列結論:①
,則下列結論:①![]() ;②當
;②當![]() 時,
時,![]() ;③點
;③點![]() 到直線
到直線![]() 的距離為
的距離為![]() ;④
;④![]() 面積的最大值是
面積的最大值是![]() .其中正確的結論是______.(填寫所有正確結論的序號)
.其中正確的結論是______.(填寫所有正確結論的序號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列關于函數![]() 的四個命題:
的四個命題:
①當x=0時,y有最小值12;
②n為任意實數,x=3+n時的函數值大于x=3-n時的函數值;
③若n>3,且n是整數,當![]() 時,y的整數值有
時,y的整數值有![]() 個;
個;
④若函數圖象過點![]() 和
和![]() ,其中a>0,b>0,則a<b.
,其中a>0,b>0,則a<b.
其中真命題的序號是( )
A.①B.②C.③D.④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com