
【題目】已知:直線![]() 與x軸、y軸分別相交于點A和點B,點C在線段AO上.將
與x軸、y軸分別相交于點A和點B,點C在線段AO上.將![]() 沿BC折疊后,點O恰好落在AB邊上點D處.
沿BC折疊后,點O恰好落在AB邊上點D處.
(1)求出OC的長?
(2)點E、F是直線BC上的兩點,若![]() 是以EF為斜邊的等腰直角三角形,求點F的坐標;
是以EF為斜邊的等腰直角三角形,求點F的坐標;
(3)取AB的中點M,若點P在y軸上,點Q在直線AB上,是否存在以C、M、P、Q為頂點的四邊形為平行四邊形?若存在,請求出所有滿足條件的Q點坐標;若不存在,請說明理由.


【答案】(1)OC的長為3;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先根據一次函數的解析式可得點A、B坐標,從而可得OA、OB、AB的長,再根據折疊的性質可得![]() ,然后在
,然后在![]() 中,利用勾股定理即可得;
中,利用勾股定理即可得;
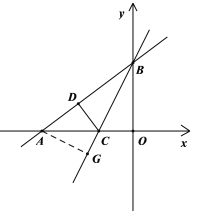
(2)如圖,先由(1)得出點C坐標,再利用待定系數法可求出直線BC的函數解析式,從而可得出直線AG的函數解析式,然后聯立直線BC、AG的函數解析式可求出點G的坐標,從而可得AG的長,最后根據等腰直角三角形的性質可得![]() ,由此建立方程求解即可得;
,由此建立方程求解即可得;
(3)先求出點M坐標,再利用待定系數法可求出直線CM的函數解析式,設點Q的坐標為![]() ,然后分MQ為所構成的平行四邊形的邊和MQ為所構成的平行四邊形的對角線兩種情況,分別根據平行四邊形的性質、兩點之間的距離公式列出等式求解即可.
,然后分MQ為所構成的平行四邊形的邊和MQ為所構成的平行四邊形的對角線兩種情況,分別根據平行四邊形的性質、兩點之間的距離公式列出等式求解即可.
(1)對于![]()
當![]() 時,
時,![]() ,解得
,解得![]() ,則點A坐標為
,則點A坐標為![]()
當![]() 時,
時,![]() ,則點B坐標為
,則點B坐標為![]()
![]()
![]()
![]()
由折疊的性質得:![]()
![]() ,
,![]()
設![]() ,則
,則![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
故OC的長為3;
(2)由(1)可得:點C坐標為![]()
設直線BC的解析式為![]()
將點![]() ,
,![]() 代入得:
代入得: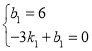 ,解得
,解得![]()
則直線BC的解析式為![]()
如圖,過點A作直線BC的垂線,交直線BC于點G
則可設直線AG的解析式為![]()
將點![]() 代入得:
代入得:![]() ,解得
,解得![]()
則直線AG的解析式為![]()
聯立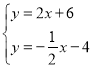 ,解得
,解得![]()
即點G坐標為![]()
由兩點之間的距離公式得:![]()
![]() 點E、F是直線BC上的兩點,且
點E、F是直線BC上的兩點,且![]() 是以EF為斜邊的等腰直角三角形
是以EF為斜邊的等腰直角三角形
![]()
設點F的坐標為![]()
則有![]()
整理得:![]()
解得![]() 或
或![]()
當![]() 時,
時,![]()
當![]() 時,
時,![]()
則點F的坐標為![]() 或
或![]() ;
;
(3)由題意得:點M坐標為![]() ,即
,即![]()
設直線CM的函數解析式為![]()
將點![]() 、
、![]() 代入得:
代入得: ,解得
,解得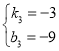
則直線CM的函數解析式為![]()
![]()
因為點Q在直線AB:![]() 上
上
所以可設點Q的坐標為![]()
由平行四邊形的定義,分以下兩種情況:
①MQ為所構成的平行四邊形的邊,則![]()
設直線CP的函數解析式為![]()
將點![]() 代入得:
代入得:![]() ,解得
,解得![]()
則直線CP的函數解析式為![]()
當![]() 時,
時,![]() ,則此時點P坐標為
,則此時點P坐標為![]()
由兩點之間的距離公式得:![]()
則![]()
解得![]() 或
或![]()
當![]() 時,
時,![]()
當![]() 時,
時,![]()
因此,此時點Q的坐標為![]() 或
或![]()
②MQ為所構成的平行四邊形的對角線,則![]()
設直線PQ的函數解析式為![]()
將點![]() 代入得:
代入得:![]() ,解得
,解得![]()
則直線PQ的函數解析式為![]()
當![]() 時,
時,![]() ,則此時點P坐標為
,則此時點P坐標為![]()
由兩點之間的距離公式得:![]()
解得![]() 或
或![]()
當![]() 時,
時,![]()
此時點Q的坐標為![]() ,點P的坐標為
,點P的坐標為![]() ,則MQ不是所構成的平行四邊形的對角線,不符題設,舍去
,則MQ不是所構成的平行四邊形的對角線,不符題設,舍去
當![]() 時,
時,![]()
因此,此時點Q的坐標為![]()
綜上,所求的點Q的坐標為![]() 或
或![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】.如圖,一條生產線的流水線上依次有5個機器人,它們站立的位置在數軸上依次用點A1,A2,A3,A4,A5表示.
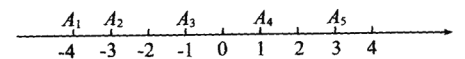
(1)若原點是零件的供應點,5個機器人分別到供應點取貨的總路程是多少?
(2)若將零件的供應點改在A1,A3,A5中的其中一處,并使得5個機器人分別到達供應點取貨的總路程最短,你認為應該在哪個點上?通過計算說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,以點B為圓心,任意長為半徑畫弧,分別交AB、BC于點M、N分別以點M、N為圓心,以大于![]() MN的長度為半徑畫弧兩弧相交于點P過點P作線段BD,交AC于點D,過點D作DE⊥AB于點E,則下列結論①CD=ED;②∠ABD=
MN的長度為半徑畫弧兩弧相交于點P過點P作線段BD,交AC于點D,過點D作DE⊥AB于點E,則下列結論①CD=ED;②∠ABD=![]() ∠ABC;③BC=BE;④AE=BE中,一定正確的是( )
∠ABC;③BC=BE;④AE=BE中,一定正確的是( )
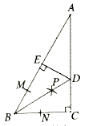
A. ①②③B. ① ② ④C. ①③④D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
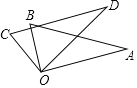
【題目】如圖,在直角坐標系中,正方形OABC的頂點B的坐標為(3,3),直線CD交直線OA于點D,直線OE交線段AB于E,且CD⊥OE,垂直為點F,若圖中陰影部分的面積是正方形OABC的面積的![]() ,則△OFC的周長為________.
,則△OFC的周長為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,OABC是平行四邊形,對角線OB在軸正半軸上,位于第一象限的點A和第二象限的點C分別在雙曲線y=![]() 和y=
和y=![]() 的一支上,分別過點A、C作x軸的垂線,垂足分別為M和N,則有以下的結論:①
的一支上,分別過點A、C作x軸的垂線,垂足分別為M和N,則有以下的結論:①![]() ;②陰影部分面積是
;②陰影部分面積是![]() (k1+k2);③當∠AOC=90°時,|k1|=|k2|;④若OABC是菱形,則兩雙曲線既關于x軸對稱,也關于y軸對稱.其中正確的結論是( )
(k1+k2);③當∠AOC=90°時,|k1|=|k2|;④若OABC是菱形,則兩雙曲線既關于x軸對稱,也關于y軸對稱.其中正確的結論是( )

A.①②B.①④C.③④D.①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則下列結論:①當x≥1時,y隨x的增大而減小;②b+2a=0;③x=3是關于x的方程ax2+bx+c=0(a≠0)的一個根;④4a-2b+c<0.其中正確的是________(填序號).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C在以AB為直徑的半圓上,AB=8,∠CBA=30°,點D在線段AB上運動,點E與點D關于AC對稱,DF⊥DE于點D,并交EC的延長線于點F.下列結論:
①CE=CF;
②線段EF的最小值為![]() ;
;
③當AD=2時,EF與半圓相切;
④若點F恰好落在B C上,則AD=![]() ;
;
⑤當點D從點A運動到點B時,線段EF掃過的面積是![]() .
.
其中正確結論的序號是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將兩塊直角三角尺的直角頂點O疊放在一起.
(1)如果∠BOD=60°,那么∠AOC= ,如果∠AOC=130°,那么∠BOD= .
(2)猜想∠AOC與∠BOD的數量關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com