
【題目】“全民閱讀”深入人心,讀好書讓人終身受益.為打造書香校園,滿足同學們的讀書需求,學校圖書館準備到新華書店采購文學名著和科技閱讀兩類圖書.經了解,20本文學名著和40本科技閱讀共需1520元,一本文學名著比一本科技閱讀多22元(注:所采購的文學名著書價格都一樣,所采購的科技閱讀書價格都一樣).
(1)求每本文學名著和科技閱讀各多少元?
(2)若學校要求購買科技閱讀比文學名著多20本,科技閱讀和文學名著總數不低于72本,總費用不超過2000元,請你為學校求出符合條件的購書方案.
(3)請在(2)的條件下,請你求出此次活動學校最多需投入資金多少元?
【答案】
(1)解:設每本文學名著x元,每本科技閱讀y元,
根據題意得: ![]() ,解得:
,解得: ![]() .
.
答:每本文學名著40元,每本科技閱讀18元.
(2)解:設購買文學名著m本,則購買科技閱讀(m+20)本,
根據題意得: ![]() ,
,
解得:26≤m≤ ![]() ,
,
∵m為正整數,
∴m=26、27、28,
∴m+20=46、47、48.
∴購買方案有:方案一:購買文學名著26本、科技閱讀46本;方案二:購買文學名著27本、科技閱讀47本;方案三:購買文學名著28本、科技閱讀48本.
(3)解:設總共投入資金w元,
根據題意得:w=40m+18(m+20)=58m+360,
∵58>0,
∴當m=28時,w取最大值,最大值為1984.
∴此次活動學校最多需投入資金1984元.
【解析】(1)設每本文學名著x元,每本科技閱讀y元,根據“20本文學名著和40本科技閱讀共需1520元,一本文學名著比一本科技閱讀多22元”,即可得出關于x、y的二元一次方程組,解之即可得出結論;(2)設購買文學名著m本,則購買科技閱讀(m+20)本,根據“科技閱讀和文學名著總數不低于72本,總費用不超過2000元”,即可得出關于m的一元一次不等式組,解之即可得出m的取值范圍,進而即可得出各種購書方案;(3)設總共投入資金w元,根據總價=單價×數量即可得出w關于m的函數關系式,再根據一次函數的性質結合m的取值范圍即可解決最值問題.
【考點精析】根據題目的已知條件,利用一元一次不等式組的應用的相關知識可以得到問題的答案,需要掌握1、審:分析題意,找出不等關系;2、設:設未知數;3、列:列出不等式組;4、解:解不等式組;5、檢驗:從不等式組的解集中找出符合題意的答案;6、答:寫出問題答案.


科目:初中數學 來源: 題型:
【題目】如圖①,一張四邊形紙片ABCD,∠A=50°,∠C=150°.若將其按照圖②所示方式折疊后,恰好MD′∥AB,ND′∥BC,則∠D的度數為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知a+b=1,ab=-1.設![]()
(1)計算S2;
(2)請閱讀下面計算S3的過程: ![]()
=![]()
=![]()
=![]()
∵a+b=1,ab=-1,
∴![]() _______.
_______.
你讀懂了嗎?請你先填空完成(2)中S3的計算結果;再計算S4;
(3)猜想并寫出![]() ,
, ![]() ,
, ![]() 三者之間的數量關系(不要求證明,且n是不小于2的自然數),根據得出的數量關系計算S3.
三者之間的數量關系(不要求證明,且n是不小于2的自然數),根據得出的數量關系計算S3.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在下列條件中,不能證明△ABD≌△ACD的是( )
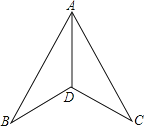
A. BD=DC,AB=AC B. ∠B=∠C,BD=DC
C. ∠B=∠C,∠BAD=∠CAD D. ∠ADB=∠ADC,BD=DC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,E是⊙O外一點,過點E作⊙O的兩條切線ED、EB,切點分別為點D,B,連接AD并延長交BE延長線于點C,連接OE. 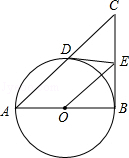
(1)試判斷OE與AC的關系,并說明理由;
(2)填空: ①當∠BAC=時,四邊形ODEB是正方形.
②當∠BAC=30°時, ![]() 的值為 .
的值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平行四邊形ABCD的兩個頂點A、C在反比例函數y= ![]() (k≠0)圖象上,點B、D在x軸上,且B、D兩點關于原點對稱,AD交y軸于P點
(k≠0)圖象上,點B、D在x軸上,且B、D兩點關于原點對稱,AD交y軸于P點 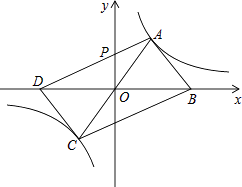
(1)已知點A的坐標是(2,3),求k的值及C點的坐標;
(2)在(1)的條件下,若△APO的面積為2,求點D到直線AC的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)與x軸交于點A(1,0)、B(3,0)兩點,與y軸交于點C(0,3).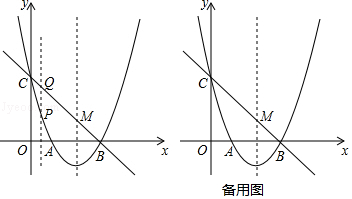
(1)求拋物線的解析式;
(2)設點P是位于直線BC下方的拋物線上一動點,過點P作y軸的平行線交直線BC于點Q,求線段PQ的最大值;
(3)在(2)的條件下,拋物線的對稱軸與直線BC交于點M,問是否存在點P,使以M、P、Q為頂點的三角形與△CBO相似?若存在,請求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com