
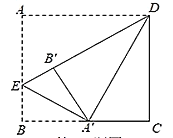
【題目】如圖,在矩形![]() 中,
中,![]() .將
.將![]() 向內翻折,點
向內翻折,點 ![]() 落在
落在![]() 上,記為
上,記為![]() ,折痕為
,折痕為![]() .若將
.若將![]() 沿
沿![]() 向內翻折,點
向內翻折,點![]() 恰好 落在
恰好 落在![]() 上,記為
上,記為![]() ,則
,則![]() 的長為( )
的長為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
首先根據矩形和翻折的性質得出△AED≌△A'ED,△A'BE≌△A'B'E,∠A'B'E=∠B=∠A'B'D=90°,∠AED=∠A'ED,∠A'EB=∠A'EB',BE=B'E,進而得出∠AED=∠A'ED=∠A'EB=60°,∠ADE=∠A'DE=∠A'DC=30°,判定△DB'A'≌△DCA',DC=DB',得出AE,設AB=DC=x,利用勾股定理構建方程,即可得解.
∵四邊形ABCD為矩形,
∴∠ADC=∠C=∠B=90°,AB=DC,
由翻折知,△AED≌△A'ED,△A'BE≌△A'B'E,∠A'B'E=∠B=∠A'B'D=90°,
∴∠AED=∠A'ED,∠A'EB=∠A'EB',BE=B'E,
∴∠AED=∠A'ED=∠A'EB=![]() ×180°=60°,
×180°=60°,
∴∠ADE=90°﹣∠AED=30°,∠A'DE=90°﹣∠A'EB=30°,
∴∠ADE=∠A'DE=∠A'DC=30°,
又∵∠C=∠A'B'D=90°,DA'=DA',
∴△DB'A'≌△DCA'(AAS),
∴DC=DB',
在Rt△AED中,
∠ADE=30°,AD=2,
∴AE=![]() ,
,
設AB=DC=x,則BE=B'E=x﹣![]()
∵AE2+AD2=DE2,
∴(![]() )2+22=(x+x﹣
)2+22=(x+x﹣![]() )2,
)2,
解得,x1=![]() (負值舍去),x2=
(負值舍去),x2=![]() ,
,
故答案為B.


科目:初中數學 來源: 題型:
【題目】如圖1,在△ABC中,AC=nAB,∠CAB=α,點E,F分別在AB,AC上且EF∥BC,把△AEF繞點A順時針旋轉到如圖2的位置.連接CF,BE.

(1)求證:∠ACF=∠ABE;
(2)若點M,N分別是EF,BC的中點,當α=90°時,求證:BE2+CF2=4MN2;
(3)如圖3,點M,N分別在EF,BC上且![]() =
=![]() =
=![]() ,若n=
,若n=![]() ,α=135°,BE=
,α=135°,BE=![]() ,直接寫出MN的長.
,直接寫出MN的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,A(﹣4,﹣2),B(﹣2,﹣2),C(﹣1,0).

(1)將△ABC向右平移5個單位長度,畫出平移后的△A1B1C1;
(2)將△ABC繞點C旋轉180°,畫出旋轉后的△A2B2C,并直接寫出點A運動的路徑長;
(3)請直接寫出△B1C1B2的外心的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,兩個轉盤中指針落在每個數字上的機會相等,現同時轉動![]() 、
、![]() 兩個轉盤,停止后,指針各指向一個數字.小力和小明利用這兩個轉盤做游戲,若兩數之積為非負數則小力勝;否則,小明勝.
兩個轉盤,停止后,指針各指向一個數字.小力和小明利用這兩個轉盤做游戲,若兩數之積為非負數則小力勝;否則,小明勝.
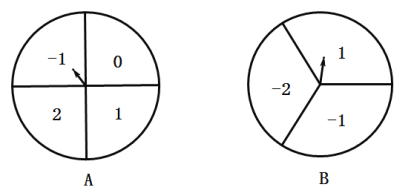
(1)畫樹狀圖或列表求出各人獲勝的概率。
(2)這個游戲公平嗎?說說你的理由
查看答案和解析>>
科目:初中數學 來源: 題型:
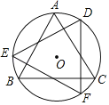
【題目】如圖,△ABC為⊙O內接等邊三角形,將△ABC繞圓心O旋轉30°到△DEF處,連接AD、AE,則∠EAD的度數為( )
A.150°B.135°C.120°D.105°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學活動課上,老師提出問題:如圖1,有一張長![]() ,寬
,寬![]()
![]() 的長方形紙板,在紙板的四個角裁去四個相同的小正方形,然后把四邊折起來,做成-一個無蓋的盒子,問小正方形的邊長為多少時,盒子的體積最大.下 面是探究過程,請補充完整:
的長方形紙板,在紙板的四個角裁去四個相同的小正方形,然后把四邊折起來,做成-一個無蓋的盒子,問小正方形的邊長為多少時,盒子的體積最大.下 面是探究過程,請補充完整:
(1)設小正方形的邊長為![]() ,體積為
,體積為![]() ,根據長方體的體積公式得到
,根據長方體的體積公式得到![]() 和
和![]() 的關系式 ;
的關系式 ;
(2)確定自變量![]() 的取值范圍是
的取值范圍是
(3)列出![]() 與
與![]() 的幾組對應值.
的幾組對應值.

| ··· |
|
|
|
|
|
|
|
|
|
|
| ··· |
|
|
|
|
|
|
|
|
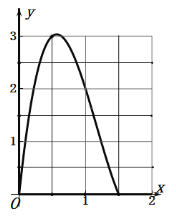
(4)在平面直角坐標系![]() 中,描出以補全后的表中各對對應值為坐標的點畫出該函數的圖象如圖2,結合畫出的函數圖象,當小正方形的邊長約為
中,描出以補全后的表中各對對應值為坐標的點畫出該函數的圖象如圖2,結合畫出的函數圖象,當小正方形的邊長約為 ![]() 時, 盒子的體積最大,最大值約為
時, 盒子的體積最大,最大值約為![]() .(估讀值時精確到
.(估讀值時精確到![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一天早上,王霞從家出發步行上學,出發6分鐘后王霞想起數學作業沒有帶,王霞立即打電話叫爸爸騎自行車把作業送來(接打電話和爸爸出門的時間忽略不計),同時王霞把速度降低到前面的一半.爸爸騎自行車追上王霞后立即掉頭以原速趕往位于家的另一邊的單位上班,王霞拿到作業后立即改為慢跑上學,慢跑的速度是最開始步行速度的2倍,最后王霞比爸爸早10分鐘到達目的地.如圖反映了王霞與爸爸之間的距離![]() (米)與王霞出發后時間
(米)與王霞出發后時間![]() (分鐘)之間的關系,則王霞的家距離學校有__________米.
(分鐘)之間的關系,則王霞的家距離學校有__________米.
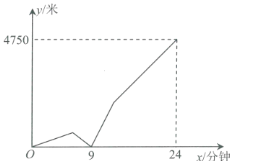
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】端午節“賽龍舟,吃粽子”是中華民族的傳統習俗.節日期間,小邱家包了三種不同餡的粽子,分別是:紅棗粽子(記為A),豆沙粽子(記為B),肉粽子(記為C),這些粽子除了餡不同,其余均相同.粽子煮好后,小邱的媽媽給一個白盤中放入了兩個紅棗粽子,一個豆沙粽子和一個肉粽子;給一個花盤中放入了兩個肉粽子,一個紅棗粽子和一個豆沙粽子.
根據以上情況,請你回答下列問題:
(1)假設小邱從白盤中隨機取一個粽子,恰好取到紅棗粽子的概率是多少?
(2)若小邱先從白盤里的四個粽子中隨機取一個粽子,再從花盤里的四個粽子中隨機取一個粽子,請用列表法或畫樹狀圖的方法,求小邱取到的兩個粽子中一個是紅棗粽子、一個是豆沙粽子的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 和點
和點![]() .(1)已知點
.(1)已知點![]() 在第一象限的拋物線上,則點
在第一象限的拋物線上,則點![]() 的坐標是_______.(2)在(l)的條件下連接
的坐標是_______.(2)在(l)的條件下連接![]() ,
,![]() 為拋物線上一點且
為拋物線上一點且![]()
![]() ,則點
,則點![]() 的坐標是_______.
的坐標是_______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com