
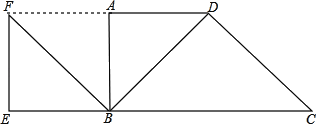
【題目】在直角梯形ABCD中,AD∥BC,∠DAB=90°,AD=1,BC=2.連接BD,把△ABD繞著點B逆時針旋轉90°得到△EBF,若點F剛好落在DA的延長線上,則∠C=________°.
【答案】45
【解析】
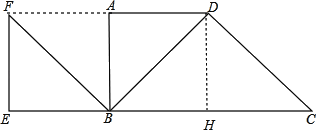
作DH⊥BC于H,如圖,易得四邊形ABHD為矩形,則BH=AD=1,AB=DH,所以HC=BC﹣BH=1,再根據旋轉的性質得∠FBD=90°,BF=BD,則可判斷△BDF為等腰直角三角形,所以BA⊥DF,根據等腰直角三角形的性質得AB=AF=AD=1,則DH=1,然后再判斷△DHC為等腰直角三角形,于是可得∠C=45°.
解:作DH⊥BC于H,如圖,
∵AD∥BC,∠DAB=90°,
∴四邊形ABHD為矩形,
∴BH=AD=1,AB=DH,
∴HC=BC﹣BH=2﹣1=1,
∵△ABD繞著點B逆時針旋轉90°得到△EBF,
∴∠FBD=90°,BF=BD,
∴△BDF為等腰直角三角形,
∵點F剛好落在DA的延長線上,
∴BA⊥DF,
∴AB=AF=AD=1,
∴DH=1,
∴△DHC為等腰直角三角形,
∴∠C=45°.
故答案為45.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】下列命題中,①等腰三角形兩腰上的高相等;②在空間中,垂直于同一直線的兩直線平行;③兩條直線被第三條直線所截,內錯角相等;④一個角的兩邊與另一個角的兩邊分別平行, 則這兩個角相等. 其中真命題的個數有 __________個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】古希臘著名的畢達哥拉斯學派把1,3,6,10…這樣的數稱為“三角形數”,而把1,4,9,16…這樣的數稱為“正方形數”.從圖中可以發現,任何一個大于1的“正方形數”都可以看作兩個相鄰“三角形數”之和.下列等式中,符合這一規律的是( )
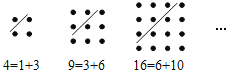
A.13=3+10B.25=9+16C.36=15+21D.49=18+31
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A是一次函數y=﹣![]() x+
x+![]() 的圖象與反比例函數y=
的圖象與反比例函數y=![]() (m>0)的圖象的一個交點,AB⊥x軸,垂足為B,且AB=
(m>0)的圖象的一個交點,AB⊥x軸,垂足為B,且AB=![]() .
.
(1)求這個反比例函數的解析式;
(2)當1<x<4,求反比例函數y=![]() 的取值范圍.
的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場銷售兩種型號的飲水機,八月份銷售A種型號的飲水機150個和B種型號的飲水機200個.
(1)商場八月份銷售飲水機時,A種型號的售價比B種型號的2倍少10元,總銷售額為88500元,那么B種型號的飲水機的單價是每件多少元?
(2)為了提高銷售量,商場九月份銷售飲水機時,A種型號的售價比八月份A種型號售價下降了![]() a%(a>0),且A種型號的銷量比八月份A種型號的銷量提高了a%;B種型號的售價比八月份的B種型號的售價下降了a%,但B種型號的銷售量與八月份的銷售量相同,結果九月份的總銷售額也是88500元,求a的值.
a%(a>0),且A種型號的銷量比八月份A種型號的銷量提高了a%;B種型號的售價比八月份的B種型號的售價下降了a%,但B種型號的銷售量與八月份的銷售量相同,結果九月份的總銷售額也是88500元,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場為了吸引顧客,設計了一種促銷活動:在一個不透明的箱子里放有4個相同的小球,球上分別標有“0元”、“10元”、“20元”和“30元”的字樣.規定:顧客在本商場同一日內,每消費滿200元,就可以在箱子里先后摸出兩個球(第一次摸出后不放回),商場根據兩小球所標金額的和返還相應價格的購物券,可以重新在本商場消費,某顧客剛好消費200元.
(1)該顧客至少可得到_____元購物券,至多可得到_______元購物券;
(2)請你用畫樹狀圖或列表的方法,求出該顧客所獲得購物券的金額不低于30元的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
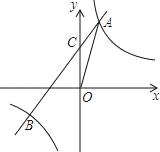
【題目】如圖,反比例函數y=![]() 的圖象與一次函數y=kx+b的圖象交于點A(m,2),點B(﹣2,n ),一次函數圖象與y軸的交點為C.
的圖象與一次函數y=kx+b的圖象交于點A(m,2),點B(﹣2,n ),一次函數圖象與y軸的交點為C.
(1)求一次函數解析式;
(2)求C點的坐標;
(3)求△AOB的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com