
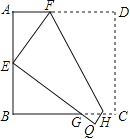
【題目】如圖,將邊長為6的正方形ABCD折疊,使點D落在AB邊的中點E處,折痕為FH,點C落在點Q處,EQ與BC交于點G,則△EBG的周長是 cm.
【答案】12
【解析】
試題根據翻折的性質可得DF=EF,設EF=x,表示出AF,然后利用勾股定理列方程求出x,從而得到AF、EF的長,再求出△AEF和△BGE相似,根據相似三角形對應邊成比例列式求出BG、EG,然后根據三角形周長的定義列式計算即可得解.
解:由翻折的性質得,DF=EF,
設EF=x,則AF=6﹣x,
∵點E是AB的中點,
∴AE=BE=![]() ×6=3,
×6=3,
在Rt△AEF中,AE2+AF2=EF2,
即32+(6﹣x)2=x2,
解得x=![]() ,
,
∴AF=6﹣![]() =
=![]() ,
,
∵∠FEG=∠D=90°,
∴∠AEF+∠BEG=90°,
∵∠AEF+∠AFE=90°,
∴∠AFE=∠BEG,
又∵∠A=∠B=90°,
∴△AEF∽△BGE,
∴![]() =
=![]() =
=![]() ,
,
即![]() =
=![]() =
=![]() ,
,
解得BG=4,EG=5,
∴△EBG的周長=3+4+5=12.
故答案為12.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
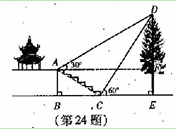
【題目】(本題7分)如圖,某校綜合實踐活動小組的同學欲測量公園內一棵樹DE的高度.他們在這棵樹正前方一座樓亭前的臺階上A點處測得樹頂端D的仰角為30°,朝著這棵樹的方向走到臺階下的點C處,測得樹頂端D的仰角為60°.已知A點的高度AB為2米,臺階AC的坡度為![]() (即AB:BC=
(即AB:BC=![]() ),且B、C、E三點在同一條盲線上。請根據以上殺件求出樹DE的高度(測傾器的高度忽略不計).
),且B、C、E三點在同一條盲線上。請根據以上殺件求出樹DE的高度(測傾器的高度忽略不計).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:我們學習過直角三角形斜邊上的中線等于斜邊的一半,即:如圖1,在![]() 中,
中,![]() ,若點
,若點![]() 是斜邊
是斜邊![]() 的中點,則
的中點,則![]()
靈活應用:如圖2,![]() 中,
中,![]() ,點
,點![]() 是
是![]() 的中點,將
的中點,將![]() 沿
沿![]() 翻折得到
翻折得到![]() 連接
連接![]() .
.
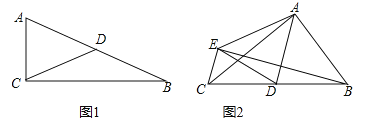
(1)線段![]() 的長是 ;
的長是 ;
(2)判斷![]() 的形狀并說明理由;
的形狀并說明理由;
(3)線段![]() 的長是 .
的長是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖正方形![]() 的頂點
的頂點![]() 是
是![]() 和
和![]() 上的動點,與
上的動點,與![]() 交于P、Q兩點,
交于P、Q兩點,![]() .
.
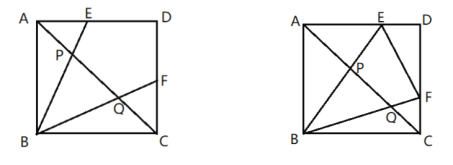
(1)當![]() 時,
時,
①求![]() 的度數;
的度數;
②求以![]() 為邊長的正方形面積;
為邊長的正方形面積;
(2)當![]() 在
在![]() 上運動時,始終保持
上運動時,始終保持![]() ,連接
,連接![]() ,則
,則![]() 面積的最小值為 (直接寫出答案).
面積的最小值為 (直接寫出答案).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b的圖象與反比例函數![]() (x>0)的圖象交于A(2,﹣1),B(
(x>0)的圖象交于A(2,﹣1),B(![]() ,n)兩點,直線y=2與y軸交于點C.
,n)兩點,直線y=2與y軸交于點C.

(1)求一次函數與反比例函數的解析式;
(2)求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 中,
中,![]() 是
是![]() 邊上的一點,
邊上的一點,![]() ,
,![]() 是
是![]() 的外接圓,
的外接圓,![]() 是
是![]() 的直徑,且交
的直徑,且交![]() 于點
于點![]() .
.
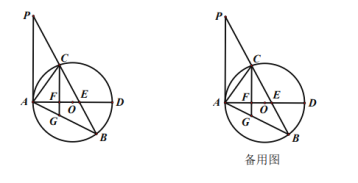
(1)求證: ![]() 是
是![]() 的切線;
的切線;
(2)過點![]() 作
作![]() 于點
于點![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() 若
若![]() 求
求![]() 的長;
的長;
(3)在滿足(2)的條件下,若![]() 求
求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,M、N分別是射線CB和射線DC上的動點,且始終∠MAN=45°.

(1)如圖1,當點M、N分別在線段BC、DC上時,請直接寫出線段BM、MN、DN之間的數量關系;
(2)如圖2,當點M、N分別在CB、DC的延長線上時,(1)中的結論是否仍然成立,若成立,給予證明,若不成立,寫出正確的結論,并證明;
(3)如圖3,當點M、N分別在CB、DC的延長線上時,若CN=CD=6,設BD與AM的延長線交于點P,交AN于Q,直接寫出AQ、AP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠MON及其邊上一點A,以點A為圓心,AO長為半徑畫弧,分別交OM,ON于點B和C,再以點C為圓心,AC長為半徑畫弧,恰好經過點B,錯誤的結論是( ).
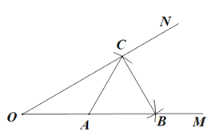
A.![]() B.∠OCB=90°C.∠MON=30°D.OC=2BC
B.∠OCB=90°C.∠MON=30°D.OC=2BC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某體育看臺側面的示意圖如圖所示,觀眾區AC的坡度i為1:2,頂端C離水平地面AB的高度為10m,從頂棚的D處看E處的仰角α=18°30′,豎直的立桿上C、D兩點間的距離為4m,E處到觀眾區底端A處的水平距離AF為3m.
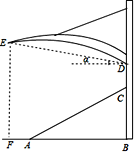
求:(1)觀眾區的水平寬度AB;
(2)頂棚的E處離地面的高度EF.(sin18°30′≈0.32,tanl8°30′≈0.33,結果精確到0.1m)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com