
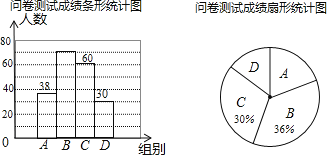
【題目】為了了解同學們對垃圾分類知識的了解程度,增強同學們的環保意識某校數學興趣小組設計了“垃圾分類知識及投放情況”問卷,并在本校隨機抽取若干名同學進行了問卷測試,根據測試成績分布情況,將測試成績分成A、B、C、D四組,繪制了如下統計圖表
問卷測試成績分組表
組別 | 分數/分 |
A | 60<x≤70 |
B | 70<x≤80 |
C | 80<x≤90 |
D | 90<x≤100 |
(1)本次抽樣調查的樣本總量是 ;
(2)樣本中,測試成績在B組的頻數是 ,D組的頻率是 ;
(3)樣本中,這次測試成績的中位數落在 組;
(4)如果該校共有880名學生,請估計成績在90<x≤100的學生約有 人.
【答案】(1)200;(2)72,0.15;(3)B;(4)132.
【解析】
(1)根據C組的人數和所占的百分比可以求得本次抽樣調查的樣本總量;
(2)根據(1)中的結果和統計圖中的數據可以分別求得測試成績在B組的頻數和D組的頻率;
(3)根據統計圖中的數據可以得到中位數落在那一組;
(4)根據統計圖中的數據可以計算出成績在90<x≤100的學生人數.
解:(1)本次抽樣調查的樣本總量是:60÷30%=200,
故答案為200;
(2)樣本中,測試成績在B組的頻數是20×36%=72,
在D組的頻率是:30÷200=0.15,
故答案為72,0.15;
(3)樣本中,這次測試成績的中位數落在B組,
故答案為B;
(4)880×![]() =132(人),
=132(人),
故答案為132.


科目:初中數學 來源: 題型:
【題目】將如圖所示的牌面數字分別是1,2,3,4的四張撲克牌背面朝上,洗勻后放在桌面上.
(1)從中隨機抽出一張牌,牌面數字是偶數的概率是__________;
(2)先從中隨機抽出一張牌,將牌面數字作為十位上的數字(不放回),再隨機抽取一張,將牌面數字作為個位上的數字,請用畫樹狀圖或列表的方法求組成的兩位數恰好是3的倍數的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() .
.![]() 于
于![]() .
.![]() 為邊
為邊![]() 上的一個(不與
上的一個(不與![]() 、
、![]() 重合)點,且
重合)點,且![]() 于
于![]() 相交于點
相交于點![]() .
.

(1)填空:![]() ______;
______;![]() ______.
______.
(2)當![]() 時,證明:
時,證明:![]() .
.
(3)![]() 面積的最小值是_______.
面積的最小值是_______.
(4)當![]() 的內心在
的內心在![]() 的外部時,直接寫出
的外部時,直接寫出![]() 的范圍______.
的范圍______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為鼓勵大學畢業生自主創業,某市政府出臺了相關政策:由政府協調,本市企業按成本價提供產品給大學畢業生自主銷售,成本價與出廠價之間的差價由政府承擔.李明按照相關政策投資銷售本市生產的一種新型節能燈.已知這種節能燈的成本價為每件8元,出廠價為每件10元,每月銷售量y(件)與銷售單價x(元)之間的關系近似滿足一次函數:y=-10x+500.
(1)李明在開始創業的第一個月將銷售單價定為20元,那么政府這個月為他承擔的總差價為多少元?
(2)設李明獲得的利潤為w(元),當銷售單價定為多少元時,每月可獲得最大利潤?
(3)物價部門規定,這種節能燈的銷售單價不得高于25元.如果李明想要每月獲得的利潤不低于3410元,那么政府為他承擔的總差價最少為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國中東部地區霧霾天氣趨于嚴重,環境治理已刻不容緩.我市某電器商場根據民眾健康需要,代理銷售某種家用空氣凈化器,其進價是![]() 元
元![]() 臺經過市場銷售后發現:在一個月內,當售價是
臺經過市場銷售后發現:在一個月內,當售價是![]() 元
元![]() 臺時,可售出
臺時,可售出![]() 臺,且售價每降低
臺,且售價每降低![]() 元,就可多售出
元,就可多售出![]() 臺.若供貨商規定這種空氣凈化器售價不能低于
臺.若供貨商規定這種空氣凈化器售價不能低于![]() 元
元![]() 臺,代理銷售商每月要完成不低于
臺,代理銷售商每月要完成不低于![]() 臺的銷售任務.
臺的銷售任務.
(1)試確定月銷售量![]() (臺)與售價
(臺)與售價![]() (元
(元![]() 臺)之間的函數關系式;
臺)之間的函數關系式;
(2)求售價![]() 的范圍;
的范圍;
(3)當售價![]() (元
(元![]() 臺)定為多少時,商場每月銷售這種空氣凈化器所獲得的利潤
臺)定為多少時,商場每月銷售這種空氣凈化器所獲得的利潤![]() (元)最大?最大利潤是多少?
(元)最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,矩形ABCD中,AB=5,BC=8,點P為BC上一動點(不與端點重合),連接AP,將△ABP沿著AP折疊.點B落到M處,連接BM、CM,若△BMC為等腰三角形,則BP的長度為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
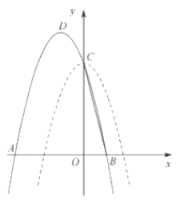
【題目】如圖,將拋物線![]() 平移后,新拋物線經過原拋物線的頂點
平移后,新拋物線經過原拋物線的頂點![]() ,新拋物線與
,新拋物線與![]() 軸正半軸交于點
軸正半軸交于點![]() ,聯結
,聯結![]() ,
,![]() ,設新拋物線與
,設新拋物線與![]() 軸的另一交點是
軸的另一交點是![]() ,新拋物線的頂點是
,新拋物線的頂點是![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)設點![]() 在新拋物線上,聯結
在新拋物線上,聯結![]() ,如果
,如果![]() 平分
平分![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)在(2)的條件下,將拋物線![]() 沿
沿![]() 軸左右平移,點
軸左右平移,點![]() 的對應點為
的對應點為![]() ,當
,當![]() 和
和![]() 相似時,請直接寫出平移后得到拋物線的表達式.
相似時,請直接寫出平移后得到拋物線的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從江岸區某初中九年級1200名學生中隨機選取一部分學生進行調查,調查情況:A、上網時間≤1小時;B、1小時<上網時間≤4小時;C、4小時<上網時間≤7小時;D、上網時間>7小時.統計結果制成了如圖統計圖:以下結論中正確的個數是( )
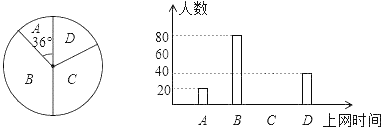
①參加調查的學生有200人;
②估計校上網不超過7小時的學生人數是900;
③C的人數是60人;
④D所對的圓心角是72°.
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
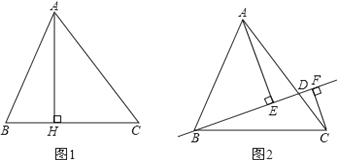
【題目】如圖1和圖2,在△ABC中,AB=13,BC=14,![]() .
.
探究:如圖1,AH⊥BC于點H,則AH=___,AC=___,△ABC的面積![]() =___.
=___.
拓展:如圖2,點D在AC上(可與點A、C重合),分別過點A、C作直線BD的垂線,垂足為E、F,設BD=x,AE=m,CF=n,(當點D與A重合時,我們認為![]() =0).
=0).
(1)用含x、m或n的代數式表示![]() 及
及![]() ;
;
(2)求(m+n)與x的函數關系式,并求(m+n)的最大值和最小值;
(3)對給定的一個x值,有時只能確定唯一的點D,指出這樣的x的取值范圍.
發現:請你確定一條直線,使得A、B、C三點到這條直線的距離之和最小(不必寫出過程),并寫出這個最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com