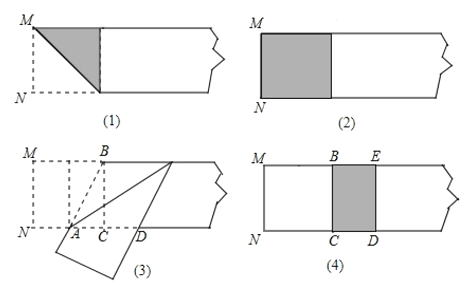
【題目】我們做個折紙游戲：第一步：在一張矩形紙片的一端，利用圖
的方法折出一個正方形，然后把紙片展開；第二步：如圖
，把這個正方形折成兩個相等的矩形，再把紙片展開；第三步：折出內側矩形的對角線
，并把它折到圖
中所示的
處；第四步：如圖
， 展平紙片，按照所得的
點折出
．則矩形
的寬
與長
的比是__________．
科目：初中數學 來源： 題型：
【題目】教材在探索平方差公式時利用了面積法，面積法除了可以幫助我們記憶公式，還可以直觀地推導或驗證公式，俗稱“無字證明”，例如，著名的趙爽弦圖（如圖①，其中四個直角三角形較大的直角邊長都為
，較小的直角邊長都為
，斜邊長都為
），大正方形的面積可以表示為
，也可以表示為
，由此推導出重要的勾股定理：如果直角三角形兩條直角邊長為
，斜邊長為，則
．
（1）圖②為美國第二十任總統伽菲爾德的“總統證法”，請你利用圖②推導勾股定理．
（2）如圖③，在
中，
是
邊上的高，
，
，
，設
，求
的值．
（3）試構造一個圖形，使它的面積能夠解釋
，畫在如圖4的網格中，并標出字母
所表示的線段．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察下列一組圖形中點的個數，其中第1個圖中共有4個點，第2個圖中共有10個點，第3個圖中共有19個點，…，按此規律第100個圖中共有點的個數是
A. 15151B. 15152C. 15153D. 15154
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，A(a，0)，C(0，c)且滿足：(a+6)2+
＝0，長方形ABCO在坐標系中(如圖)，點O為坐標系的原點．
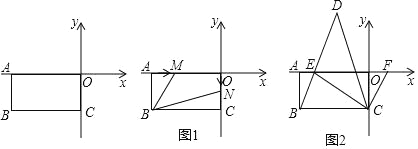
(1)求點B的坐標．
(2)如圖1，若點M從點A出發，以2個單位/秒的速度向右運動(不超過點O)，點N從原點O出發，以1個單位/秒的速度向下運動(不超過點C)，設M、N兩點同時出發，在它們運動的過程中，四邊形MBNO的面積是否發生變化？若不變，求其值；若變化，求變化的范圍．
(3)如圖2，E為x軸負半軸上一點，且∠CBE＝∠CEB，F是x軸正半軸上一動點，∠ECF的平分線CD交BE的延長線于點D，在點F運動的過程中，請探究∠CFE與∠D的數量關系，并說明理由
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將平行四邊形紙片
沿對角線
翻折，使點
落在平行四邊形所在平面內，
和
相交于點
，連接
判斷和的位置關系，并證明．
在圖1中，若
，是否存在
恰好為直角三角形的情形?若存在，求出
的長度：若不存在，請說明理由．
若將圖中平行四邊形紙片換成矩形紙片，沿對角線折疊發現所得圖形是軸對稱圖形；將所得圖形沿其對稱軸再次折疊后，得到的仍是軸對稱圖形．則矩形紙片的長寬之比是多少?請直接寫出結果．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】完成下面的證明：
已知：如圖，AB∥DE，求證：∠D+∠BCD﹣∠B=180°，
證明：過點C作CF∥AB．
∵AB∥CF（已知），
∴∠B= （ ）．
∵AB∥DE，CF∥AB（ 已知 ），
∴CF∥DE （ ）
∴∠2+ =180° （ ）
∵∠2=∠BCD﹣∠1，
∴∠D+∠BCD﹣∠B=180° （ ）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列命題是真命題的是( )
A.一組對邊平行且有一組對角相等的四邊形是平行四邊形
B.對角線相等的四邊形是矩形
C.一組對邊平行且另一組對邊相等的四邊形是平行四邊形
D.對角線互相垂直且相等的四邊形是正方形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
