
【題目】閱讀資料,解決問(wèn)題.
人教版《數(shù)學(xué)九年級(jí)(下冊(cè))》的![]() 頁(yè)有這樣一個(gè)思考問(wèn)題:
頁(yè)有這樣一個(gè)思考問(wèn)題:
問(wèn)題:如圖,在![]() 中,
中,![]() 交
交![]() ,
,![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() ,如果通過(guò)“相似的定義”證明
,如果通過(guò)“相似的定義”證明![]() ?
?
根據(jù)“兩直線平行,同位角相等”容易得出三對(duì)對(duì)應(yīng)角分別相等,再根據(jù)“平行線分線段成比例”的基本事實(shí),容易得出![]() ,所以這個(gè)問(wèn)題的核心時(shí)如何證明“
,所以這個(gè)問(wèn)題的核心時(shí)如何證明“![]() ”.
”.
證明思路:過(guò)點(diǎn)![]() 作
作![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,構(gòu)造平行四邊形
,構(gòu)造平行四邊形![]() ,得到
,得到![]() ,從而將比例式中的
,從而將比例式中的![]() ,
,![]() 轉(zhuǎn)化為共線的兩條線段
轉(zhuǎn)化為共線的兩條線段![]() ,
,![]() ,同時(shí)也構(gòu)造了基本圖形“
,同時(shí)也構(gòu)造了基本圖形“ ”,得到
”,得到![]() ,從而得證.
,從而得證.

解決問(wèn)題:
(![]() )①類(lèi)比資料中的證明思路,請(qǐng)你證明“三角形內(nèi)角平分線定理”.
)①類(lèi)比資料中的證明思路,請(qǐng)你證明“三角形內(nèi)角平分線定理”.
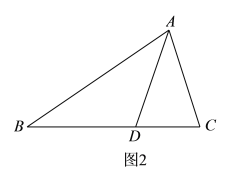
三角形內(nèi)角平分線定理:三角形的內(nèi)角平分線分對(duì)邊所得的兩條線段和這個(gè)角的兩邊對(duì)應(yīng)成比例.
已知:如圖![]() ,
,![]() 中,
中,![]() 是角平分線.
是角平分線.
求證:![]() .
.

②運(yùn)用“三角形內(nèi)角平分線定理”填空:
已知:如圖![]() ,
,![]() 中,
中,![]() 是角平分線,
是角平分線,![]() ,
,![]() ,
,![]() ,則
,則![]() __________.
__________.
(![]() )我們知道,如果兩個(gè)三角形有相同的高或者相等的高,那么它們面積的比就等于底的比.
)我們知道,如果兩個(gè)三角形有相同的高或者相等的高,那么它們面積的比就等于底的比.
請(qǐng)你通過(guò)研究![]() 和
和![]() 面積的比來(lái)證明三角形內(nèi)角平分線定理.
面積的比來(lái)證明三角形內(nèi)角平分線定理.
已知:如圖![]() ,
,![]() 中,
中,![]() 是角平分線.
是角平分線.
求證:![]() .
.

【答案】(![]() )①證明見(jiàn)解析②
)①證明見(jiàn)解析②![]() (2)證明見(jiàn)解析
(2)證明見(jiàn)解析
【解析】
(1)①如圖過(guò)點(diǎn)![]() 作
作![]() 的平行線交
的平行線交![]() 的延長(zhǎng)線于點(diǎn)
的延長(zhǎng)線于點(diǎn)![]() ,然后說(shuō)明
,然后說(shuō)明![]() ,利用相似三角形的性質(zhì)即可完成證明;②設(shè)
,利用相似三角形的性質(zhì)即可完成證明;②設(shè)![]() ,然后利用(1)的結(jié)論和已知條件即可完成解答; (
,然后利用(1)的結(jié)論和已知條件即可完成解答; (![]() )過(guò)點(diǎn)
)過(guò)點(diǎn)![]() 作
作![]() ,
,![]() 的垂線,垂足為
的垂線,垂足為![]() 、
、![]() ,
,
過(guò)點(diǎn)![]() 作
作![]() 的垂線,垂足為
的垂線,垂足為![]() ;先利用角平分線定理說(shuō)明
;先利用角平分線定理說(shuō)明![]() ,然后再利用等面積法得到
,然后再利用等面積法得到![]() 和
和![]() ,從而得到
,從而得到![]() ,即
,即![]() .
.
(![]() )①證明:過(guò)點(diǎn)
)①證明:過(guò)點(diǎn)![]() 作
作![]() 的平行線交
的平行線交![]() 的延長(zhǎng)線于點(diǎn)
的延長(zhǎng)線于點(diǎn)![]() ,
,

∴![]() ,
,
又∵![]() 平分
平分![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
②設(shè)![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() .
.

(![]() )過(guò)點(diǎn)
)過(guò)點(diǎn)![]() 作
作![]() ,
,![]() 的垂線,垂足為
的垂線,垂足為![]() 、
、![]() ,
,
過(guò)點(diǎn)![]() 作
作![]() 的垂線,垂足為
的垂線,垂足為![]() ,
,
∵![]() 為
為![]() 的角分線,
的角分線,
∴![]() ,
,
![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,二次函數(shù)![]() 圖象的頂點(diǎn)為D,其圖象與x軸的交點(diǎn)A、B的橫坐標(biāo)分別為
圖象的頂點(diǎn)為D,其圖象與x軸的交點(diǎn)A、B的橫坐標(biāo)分別為![]() 、3,與y軸負(fù)半軸交于點(diǎn)C,在下面四個(gè)結(jié)論中:
、3,與y軸負(fù)半軸交于點(diǎn)C,在下面四個(gè)結(jié)論中:
①![]() ;②
;②![]() ;
;![]() 只有當(dāng)
只有當(dāng)![]() 時(shí),
時(shí),![]() 是等腰直角三角形;其中正確的結(jié)論是__________
是等腰直角三角形;其中正確的結(jié)論是__________![]() 請(qǐng)把正確結(jié)論的序號(hào)都填上
請(qǐng)把正確結(jié)論的序號(hào)都填上![]()

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】按如圖所示的方法用小棒擺正六邊形,擺2個(gè)正六邊形要11根小棒,擺3個(gè)正六邊形要16根小棒,擺n個(gè)正六邊形需要_________根小棒.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,BD為⊙O的直徑,點(diǎn)A是弧BC的中點(diǎn),AD交BC于E點(diǎn),AE=2,ED=4. 
(1)求證: ![]() ~△ADB;
~△ADB;
(2) 求![]() 的值;
的值;
(3)延長(zhǎng)BC至F,連接FD,使![]() 的面積等于
的面積等于![]() ,求證:DF與⊙O相切。
,求證:DF與⊙O相切。
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線![]() (
(![]() ,且為常數(shù)).
,且為常數(shù)).
(![]() )求證:拋物線與
)求證:拋物線與![]() 軸有兩個(gè)公共點(diǎn).
軸有兩個(gè)公共點(diǎn).
(![]() )若拋物線與
)若拋物線與![]() 軸的一個(gè)交點(diǎn)為
軸的一個(gè)交點(diǎn)為![]() ,另一個(gè)交點(diǎn)為
,另一個(gè)交點(diǎn)為![]() ,與
,與![]() 軸交點(diǎn)為
軸交點(diǎn)為![]() ,直接寫(xiě)出直線
,直接寫(xiě)出直線![]() 與拋物線對(duì)稱(chēng)軸的交點(diǎn)
與拋物線對(duì)稱(chēng)軸的交點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】材料1新規(guī)定:求若干個(gè)相同的有理數(shù)(均不等于![]() )的除法運(yùn)算叫做除方,如
)的除法運(yùn)算叫做除方,如![]() ,
,![]() 等.類(lèi)比有理數(shù)的乘方,我們把
等.類(lèi)比有理數(shù)的乘方,我們把![]() 記作
記作![]() ,讀作“
,讀作“![]() 的圈
的圈![]() 次方”,
次方”,![]() 記作
記作![]() ,讀作“
,讀作“![]() 的圈
的圈![]() 次方”,一般地,把
次方”,一般地,把![]() 記作
記作![]() ,讀作“
,讀作“![]() 的圈
的圈![]() 次方”.我們知道,有理數(shù)的減法運(yùn)算可以轉(zhuǎn)化為加法運(yùn)算,除法運(yùn)算可以轉(zhuǎn)化為乘法運(yùn)算,有理數(shù)的除方運(yùn)算如何轉(zhuǎn)化為乘方運(yùn)算呢?
次方”.我們知道,有理數(shù)的減法運(yùn)算可以轉(zhuǎn)化為加法運(yùn)算,除法運(yùn)算可以轉(zhuǎn)化為乘法運(yùn)算,有理數(shù)的除方運(yùn)算如何轉(zhuǎn)化為乘方運(yùn)算呢?
如: 
(1)直接寫(xiě)出計(jì)算結(jié)果:  .
.
材料2 新規(guī)定:自然數(shù)1到![]() 的連乘積用表示
的連乘積用表示![]() ,例如:
,例如:![]() ,
,![]() ,
,![]() ,
,![]() ,……在這種規(guī)定下:
,……在這種規(guī)定下:
(2)仿照上面的算式,將一個(gè)非零有理數(shù)![]() 的圈
的圈![]() 次方寫(xiě)成冪的形式等于 ;
次方寫(xiě)成冪的形式等于 ;
(3)一算:
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知△ABC的三個(gè)頂點(diǎn)的坐標(biāo)分別為A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)畫(huà)出△ABC關(guān)于原點(diǎn)成中心對(duì)稱(chēng)的三角形△A′B′C′;
(2)將△ABC繞坐標(biāo)原點(diǎn)O逆時(shí)針旋轉(zhuǎn)90°,畫(huà)出圖形,直接寫(xiě)出點(diǎn)B的對(duì)應(yīng)點(diǎn)B″的坐標(biāo);
(3)請(qǐng)直接寫(xiě)出:以A、B、C為頂點(diǎn)的平行四邊形的第四個(gè)頂點(diǎn)D的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商店第一次用300元購(gòu)進(jìn)筆記本若干,第二次又用300元購(gòu)進(jìn)該款筆記本,但這次每本的進(jìn)價(jià)是第一次進(jìn)價(jià)的![]() 倍,購(gòu)進(jìn)數(shù)量比第一次少了25本.
倍,購(gòu)進(jìn)數(shù)量比第一次少了25本.
(1)求第一次每本筆記本的進(jìn)價(jià)是多少元?
(2)若要求這兩次購(gòu)進(jìn)的筆記本按同一價(jià)格全部銷(xiāo)售完畢后獲利不低于450元,問(wèn)每本筆記本的售價(jià)至少是多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】目前節(jié)能燈在城市已基本普及,某商場(chǎng)計(jì)劃購(gòu)進(jìn)甲、乙兩種節(jié)能訂共1200只,這兩種節(jié)能燈的進(jìn)價(jià)、售價(jià)如下表:
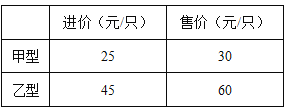
(1)如何進(jìn)貨,進(jìn)貨款恰好為46000元?
(2)為確保乙型節(jié)能燈順利暢銷(xiāo),在(1)的條件下,商家決定對(duì)乙型節(jié)能燈進(jìn)行打折出售,且全部售完后,乙型節(jié)能燈的利潤(rùn)率為20%,請(qǐng)同乙型節(jié)能燈需打幾折?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com